Particle A and B are moving in coplanar circular paths centred at O. They are totating in the same sense. Time periods of rotation of A and B around O are TA and TB, respectively, with TB>TA. Time required for B to make one ratation around O relative to A is :
TB−TA
TB+TA
TBTATB+TA
TBTATB−TA
The correct Answer is:D
To solve the problem, we need to determine the time required for particle B to make one complete rotation around point O relative to particle A.
1. Understanding the Time Periods:
- Let TA be the time period of particle A.
- Let TB be the time period of particle B.
- Given that TB>TA, this means that particle B takes longer to complete one rotation than particle A.
2. Relative Motion:
- We need to find the relative time taken by B to complete one rotation around O as observed from A's perspective.
- The angular velocity ω of a particle is given by the formula:
ω=2πT
- Therefore, the angular velocities of particles A and B are:
ωA=2πTA
ωB=2πTB
3. Relative Angular Velocity:
- The relative angular velocity of B with respect to A is given by:
ωBA=ωB−ωA
- Substituting the values of ωA and ωB:
ωBA=2πTB−2πTA
- Factoring out 2π:
ωBA=2π(1TB−1TA)
4. Time for One Complete Rotation:
- The time taken for B to complete one rotation relative to A can be found using the formula:
TBA=2πωBA
- Substituting ωBA:
TBA=2π2π(1TB−1TA)=1(1TB−1TA)
- Simplifying further:
TBA=TATBTB−TA
Final Answer:
The time required for particle B to make one rotation around O relative to particle A is:
TBA=TATBTB−TA
- Let TA be the time period of particle A.
- Let TB be the time period of particle B.
- Given that TB>TA, this means that particle B takes longer to complete one rotation than particle A.
- We need to find the relative time taken by B to complete one rotation around O as observed from A's perspective.
- The angular velocity ω of a particle is given by the formula:
ω=2πT
- Therefore, the angular velocities of particles A and B are:
ωA=2πTA
ωB=2πTB
- The relative angular velocity of B with respect to A is given by:
ωBA=ωB−ωA
- Substituting the values of ωA and ωB:
ωBA=2πTB−2πTA
- Factoring out 2π:
ωBA=2π(1TB−1TA)
- The time taken for B to complete one rotation relative to A can be found using the formula:
TBA=2πωBA
- Substituting ωBA:
TBA=2π2π(1TB−1TA)=1(1TB−1TA)
- Simplifying further:
TBA=TATBTB−TA
The time required for particle B to make one rotation around O relative to particle A is:
TBA=TATBTB−TA
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (ROTATIONAL MOTION)
72 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two small satellites are moving in circular orbits around the earth at a distance R and R+ΔR from the centre of the earth. If their time period of rotation are T and T+ΔT respectively, then
View SolutionTwo cars A and B are going around concentric circular paths of τA and τB. If the two cars complete the circular paths in the same time then the ratio of angular speeds of A and B is
View SolutionTwo particles revolve concentrically in a horizontal plane in the same direction. The time required to complete one revolution for particle A is 3min , while for particle B is 1min . The time required for A to complete one revolution relative to B is
View SolutionTwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
View SolutionIn the figure the masses of the blocks A and B are same and each equal to m. The tensions in the strings OA and AB are T2 and T1 respectively. The system is in equilibrium with a constant horizontal force mg on B. The tension T1 is :-
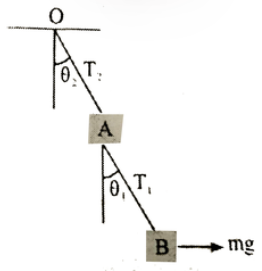
View SolutionTwo buses A and B are moving around concentric circular pathe of radii rA and rB If the two buses complete the circular paths in the sme time. The ratio on their linear speeds is
View SolutionTwo buses A and B are moving around concentric circular pathe of radii rA and rB If the two buses complete the circular paths in the sme time. The ratio on their linear speeds is
View SolutionIf for two gases of molecular weights MA and MB at temperature TA and TB, respectively, TAMB=TBMA, then which property has the same magnitude for both the gases?
View SolutionTwo particles A and B moving in a plane have velocities as shown in figure .Relative velocity of A w.r.t B
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View Solution
