A tank containing water has an orifice in one vertical side. If the centre of orifice is 4.9 m below the surface level in the tank, the velocity of discharge is:
4.9 metre/second
9.8 metre/second
2.45 metre/second
zero
The correct Answer is:B
To find the velocity of discharge from an orifice in a tank of water, we can use Bernoulli's equation. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a tank of water with an orifice located 4.9 meters below the surface of the water. We need to find the velocity of water discharging from the orifice.
Step 2: Identify Relevant Parameters
- Depth of the orifice below the water surface, h=4.9m
- Acceleration due to gravity, g=9.8m/s2
Step 3: Apply Bernoulli's Equation
Bernoulli's equation relates the pressure, velocity, and height at two points in a fluid flow. For our case, we can simplify it as follows:
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
Where:
- P1 and P2 are the pressures at points 1 and 2.
- ρ is the density of the fluid (water).
- h1 and h2 are the heights at points 1 and 2.
- v1 and v2 are the velocities at points 1 and 2.
Step 4: Set Up the Equation
At the surface of the water (point 1):
- The pressure P1=P0 (atmospheric pressure)
- The height h1=4.9m
- The velocity v1=0 (water is still)
At the orifice (point 2):
- The pressure P2=P0 (atmospheric pressure)
- The height h2=0 (reference level at the orifice)
- The velocity v2=V (unknown discharge velocity)
Step 5: Simplify the Equation
Substituting the known values into Bernoulli's equation:
P0+ρgh1+0=P0+0+12ρV2
Cancelling P0 and rearranging gives:
ρgh1=12ρV2
Step 6: Cancel Out the Density
Since ρ appears on both sides, we can cancel it out:
gh1=12V2
Step 7: Solve for Velocity V
Rearranging gives:
V2=2gh1
Taking the square root:
V=√2gh1
Step 8: Substitute the Values
Now substituting g=9.8m/s2 and h1=4.9m:
V=√2×9.8×4.9
Calculating:
V=√96.04=9.8m/s
Final Answer
The velocity of discharge is V=9.8m/s.
---
We have a tank of water with an orifice located 4.9 meters below the surface of the water. We need to find the velocity of water discharging from the orifice.
- Depth of the orifice below the water surface, h=4.9m
- Acceleration due to gravity, g=9.8m/s2
Bernoulli's equation relates the pressure, velocity, and height at two points in a fluid flow. For our case, we can simplify it as follows:
- P1 and P2 are the pressures at points 1 and 2.
- ρ is the density of the fluid (water).
- h1 and h2 are the heights at points 1 and 2.
- v1 and v2 are the velocities at points 1 and 2.
At the surface of the water (point 1):
- The pressure P1=P0 (atmospheric pressure)
- The height h1=4.9m
- The velocity v1=0 (water is still)
- The pressure P2=P0 (atmospheric pressure)
- The height h2=0 (reference level at the orifice)
- The velocity v2=V (unknown discharge velocity)
Substituting the known values into Bernoulli's equation:
Since ρ appears on both sides, we can cancel it out:
Rearranging gives:
Now substituting g=9.8m/s2 and h1=4.9m:
The velocity of discharge is V=9.8m/s.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Hydrostatics)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)
26 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
A tank containing water has an orifice 2 m below the surface of water. If there is no wastage of energy. Find the speed of discharge.
View SolutionAn engine pumps water from a tank at the rate of 10 kg per second and ejects from a nozzle 7 m above the surface of the tank with a velocity of 20 m/s. What is the output power of the engine?
View Solution
Knowledge Check
A,B, and C are the unequal faces of a rectanglular tank. The tank contains a certain amount of water. When the tank is based on the face A, the height of the water is half the height of the tank. The dimensions of the side B are 3 ft. × ft, and the dimensions of side C are 4ft×5ft, what is the measure of the hight of the water in the tank in feet?
A2B2.5C3D4
A water tank is constructed on the top of a building. With what speed will the water come out of a tap 6.0 m below the water level in the tank? Assume steady flow and that the pressure above the water level is equal to the atmospheric pressure
View SolutionA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View SolutionIf the water emerge from an orifice in a tank in which the gauge pressure is 4×105Nm−2 before the flow starts, then what will be the velocity of the water emerging out ? Take density of water is 1000kgm−3
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionA 50 L tank initailly contains 10 L of fresh water, At t=0, a brine solution containing 1 lb of salt per gallon is poured into the tank at the rate of 4 L/min, while the well-stirred mixture leaves the tank at the rate of 2 L/min. Then the amount of time required for overflow to occur in
View SolutionA tank with a small orifice contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. Assuming the level of oil outside the tank above orifice does not change.
a. What is the velocity of this flow initially?
b. When the flow stops, what would be the position of the oil-water interface in the tank?
c. Determine the time at which the flow stops. Density,of oil 800kg/m3.
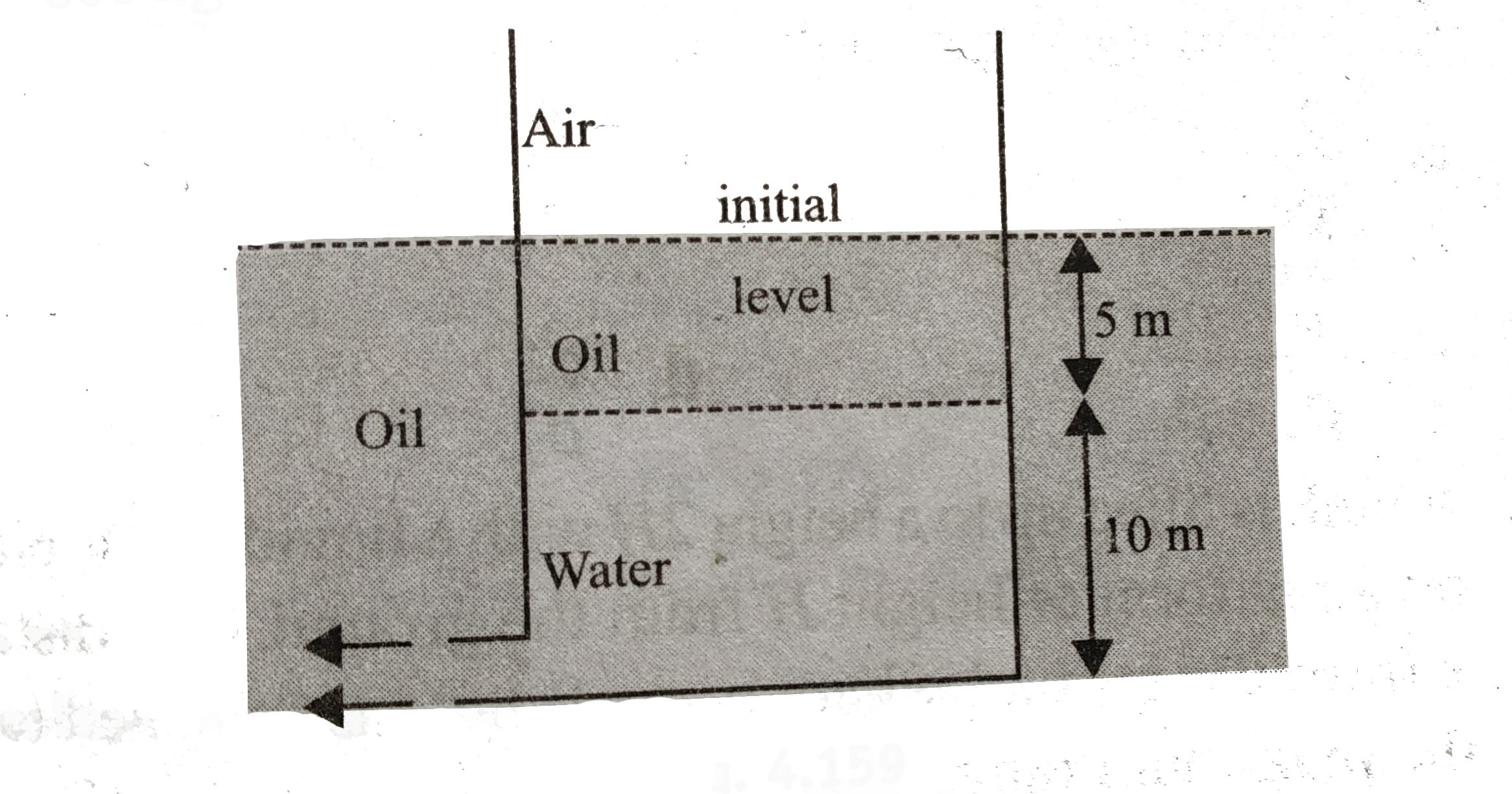
View SolutionA water tank is placed on a platform of height 5 m high and there is an orifice near the bottom in the wall of tank at 5 m below the level of water. Find the speed with which water will hit the ground [Take g = 10 m/s2 ]
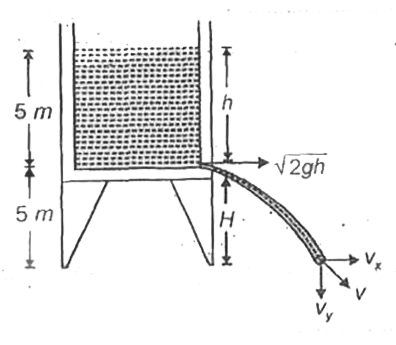
View Solution