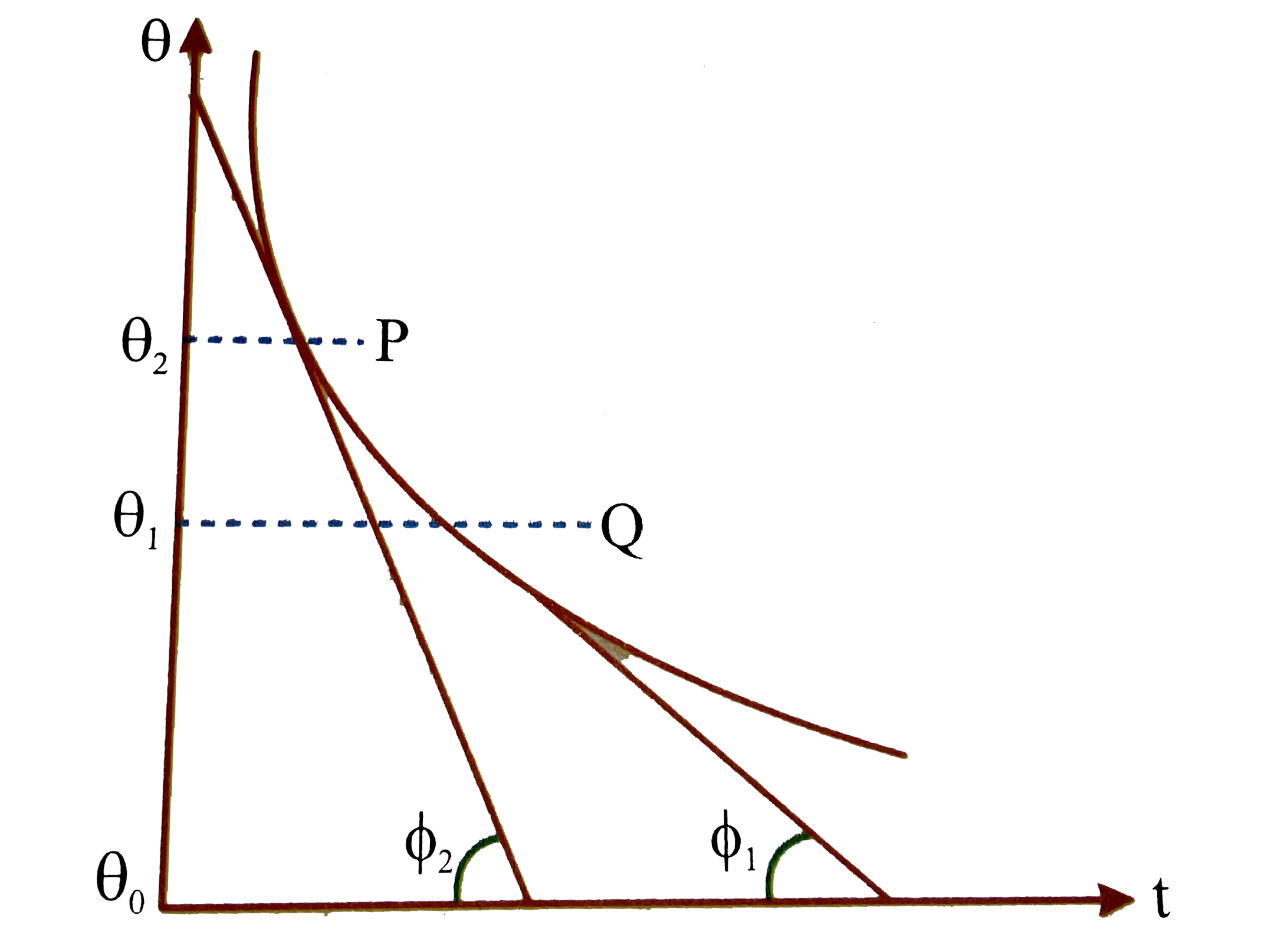
A body cools in a surrounding which is at a constant temperature of θ0. Assume that it obeys Newton's law of cooling. Its temperature θ is plotted against time t. Tangent are drawn to the curve at the points P(θ=θ2) and Q(θ=θ1). These tangents meet the time axis at angles of ϕ2 and ϕ1 as shown , then :-
_E01_113_Q01.png)
tanϕ2tanϕ1=θ1−θ0θ2−θ0
tanϕ2tanϕ1=θ2−θ0θ1−θ0
tanϕ1tanϕ2=θ1θ2
tanϕ1tanϕ2=θ2θ1
The correct Answer is:B
Step by step video solution for A body cools in a surrounding which is at a constant temperature of theta_(0). Assume that it obeys Newton's law of cooling. Its temperature theta is plotted against time t. Tangent are drawn to the curve at the points P(theta= theta_(2)) and Q(theta = theta_(1)). These tangents meet the time axis at angles of phi_(2) and phi_(1) as shown , then :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Kinetic theory of gasess)
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Thermodynamic process)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Calorimetry)
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
View SolutionA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View SolutionFind the slopes of the tangent and the normal to the curve x=a(θ−sinθ), y=a(1−cosθ) at θ=π/2
View SolutionFind the slopes of the tangent and the normal to the curve x=a(θ−sinθ) , y=a(1+cosθ) at θ=−π/2
View SolutionFind the equations of the tangent and the normal to the curve x=a(θ+sinθ), y=a(1−cosθ) at θ at indicated points.
View SolutionIn Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionThe tangents to the curve x=a(θ−sinθ),y=a(1+cosθ) at the points θ=(2k+1)π,k∈Z are parallel to :
View Solutiontangents are drawn to x2+y2=a2 at the points A(acosθ,asinθ) and B(acos(θ+π3),asin(θ+π3)) Locus of intersection of these tangents is
View SolutionIf the acute formed between y - axis and the tangent drawn to the curve y=x2+4x−17 at the point P(52,−34) is θ, the value of cotθ is equal to
View SolutionIf 3tanθtanϕ=1, then prove that 2 cos(θ+ϕ)=cos(θ−ϕ).
View Solution
