A metal rod extends on the x−axis from x=0m to x=4m. Its linear density ρ (mass/length) id not uniform and varies with the distance x from the origin according to equation ρ=(1.5+2x)kg/m What is the mass of rod:−
16kg
22kg
28kg
32kg
The correct Answer is:B
To find the mass of the metal rod, we will follow these steps:
Step 1: Understand the linear density function
The linear density ρ of the rod is given as a function of x:
ρ(x)=1.5+2x(in kg/m)
Step 2: Set up the mass element
The mass element dm of a small segment of the rod of length dx at position x can be expressed as:
dm=ρ(x)dx=(1.5+2x)dx
Step 3: Integrate to find the total mass
To find the total mass M of the rod, we need to integrate dm from x=0 to x=4:
M=∫40dm=∫40(1.5+2x)dx
Step 4: Perform the integration
Now, we will integrate the function:
M=∫40(1.5+2x)dx=∫401.5dx+∫402xdx
Calculating each integral:
1. ∫401.5dx=1.5x∣∣∣40=1.5×4−1.5×0=6
2. ∫402xdx=x2∣∣∣40=42−02=16
Adding these results together:
M=6+16=22kg
Step 5: Final answer
The total mass of the rod is:
22kg
---
The linear density ρ of the rod is given as a function of x:
ρ(x)=1.5+2x(in kg/m)
The mass element dm of a small segment of the rod of length dx at position x can be expressed as:
dm=ρ(x)dx=(1.5+2x)dx
To find the total mass M of the rod, we need to integrate dm from x=0 to x=4:
M=∫40dm=∫40(1.5+2x)dx
Now, we will integrate the function:
M=∫40(1.5+2x)dx=∫401.5dx+∫402xdx
Calculating each integral:
1. ∫401.5dx=1.5x∣∣∣40=1.5×4−1.5×0=6
2. ∫402xdx=x2∣∣∣40=42−02=16
M=6+16=22kg
The total mass of the rod is:
22kg
Topper's Solved these Questions
Similar Questions
A rod of length L is placed along the X-axis between x=0andx=L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. a.) Find the SI units of a and b b.) Find the mass of the rod in terms of a,b, and L.
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionA thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx4. Find the position of centre of mass of rod in meters.
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View Solution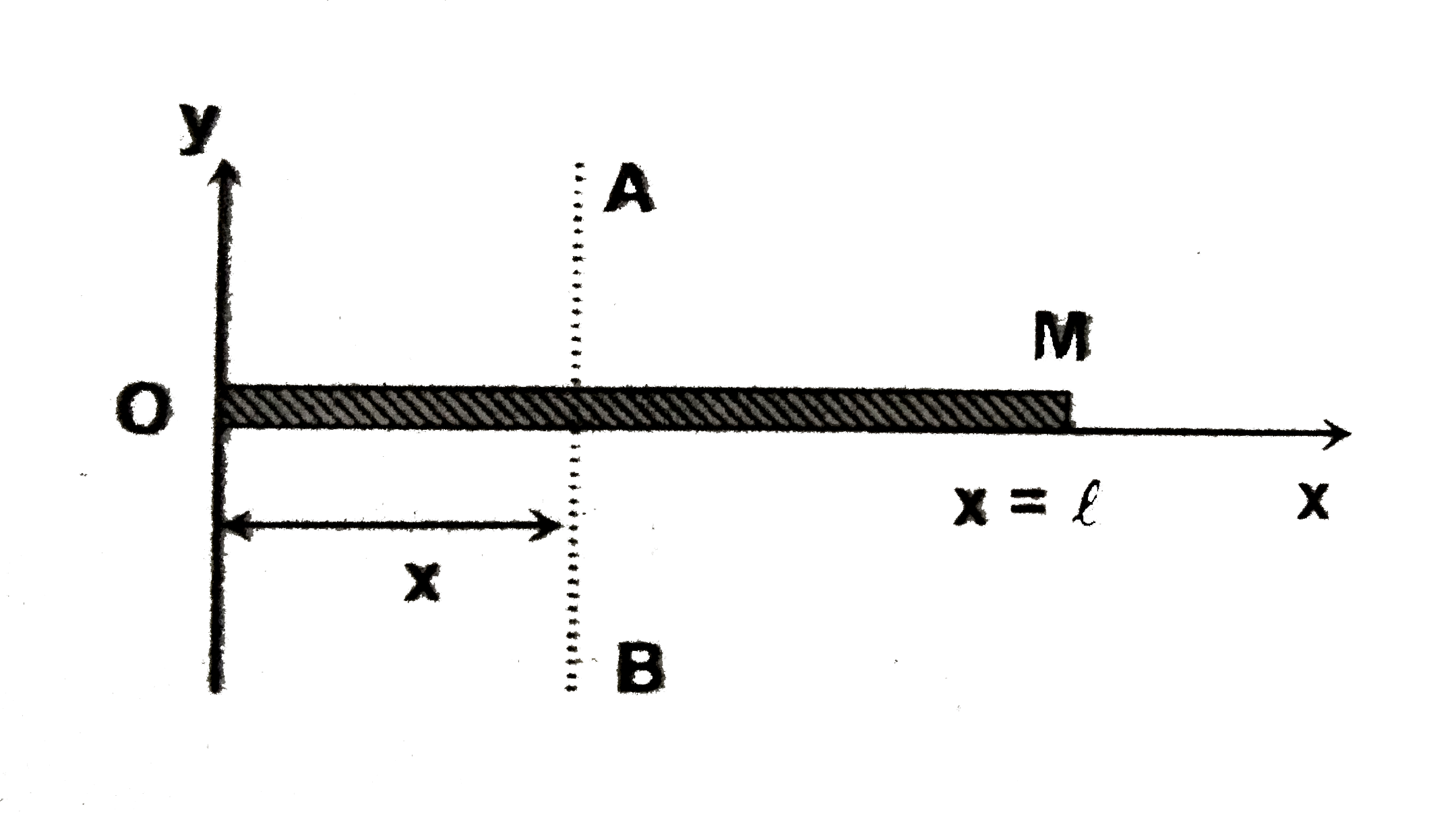
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?View Solution
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass densty that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.
 View Solution
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionIf linear density of a rod of length 3m varies as λ=2+x, them the position of the centre of gravity of the rod is
View Solution

