An infinite non-conducting plane with uniform charge density σ is kept parallel to yz plane and at a distance 'd' from a dipole →p which itself is located at the origin. An equipotential surface for this system is spherical, centred at origin, having radius R(<d). Given that R=(pnπσ)1/3, find the integer n

The correct Answer is:2
Tangential components must cancel.
⇒σ2ε0=14πε0psinθR3
⇒R3=p2πσ
⇒n=2

Similar Questions
An infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
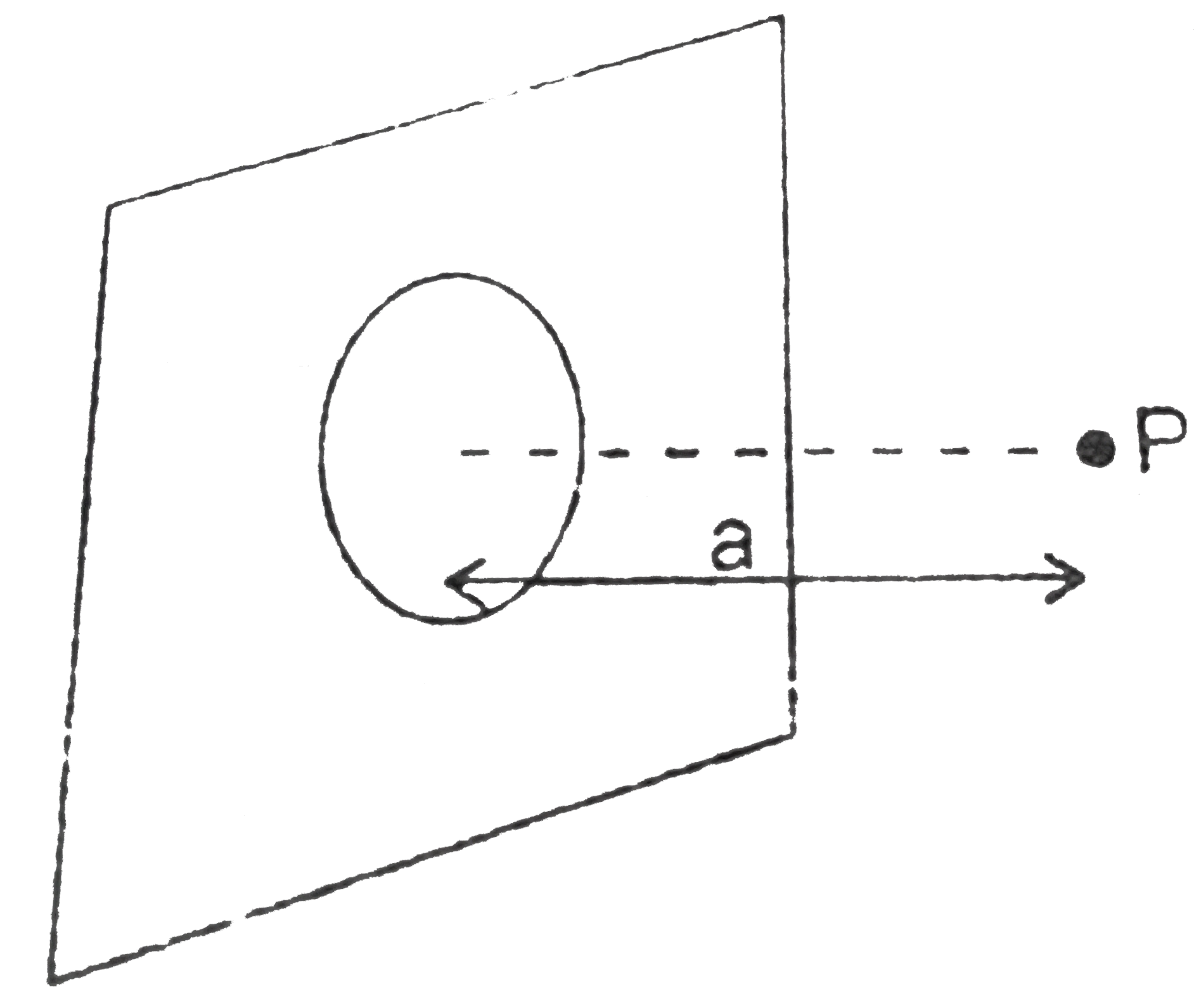
View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.

View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
A circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionAn infinite dielectric sheet having charge density σ has a holeof radius R in it. An electrom is released from point P on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the plane of the sheet.
 .
.
View Solution
An infinite non-conducting plate of charge has thickness d and contains uniform charge distribution fo charge density, which one of the following graphs represents the variation of electric field E(x) with x. (here x is the distance from central plane of non-conducting plate)
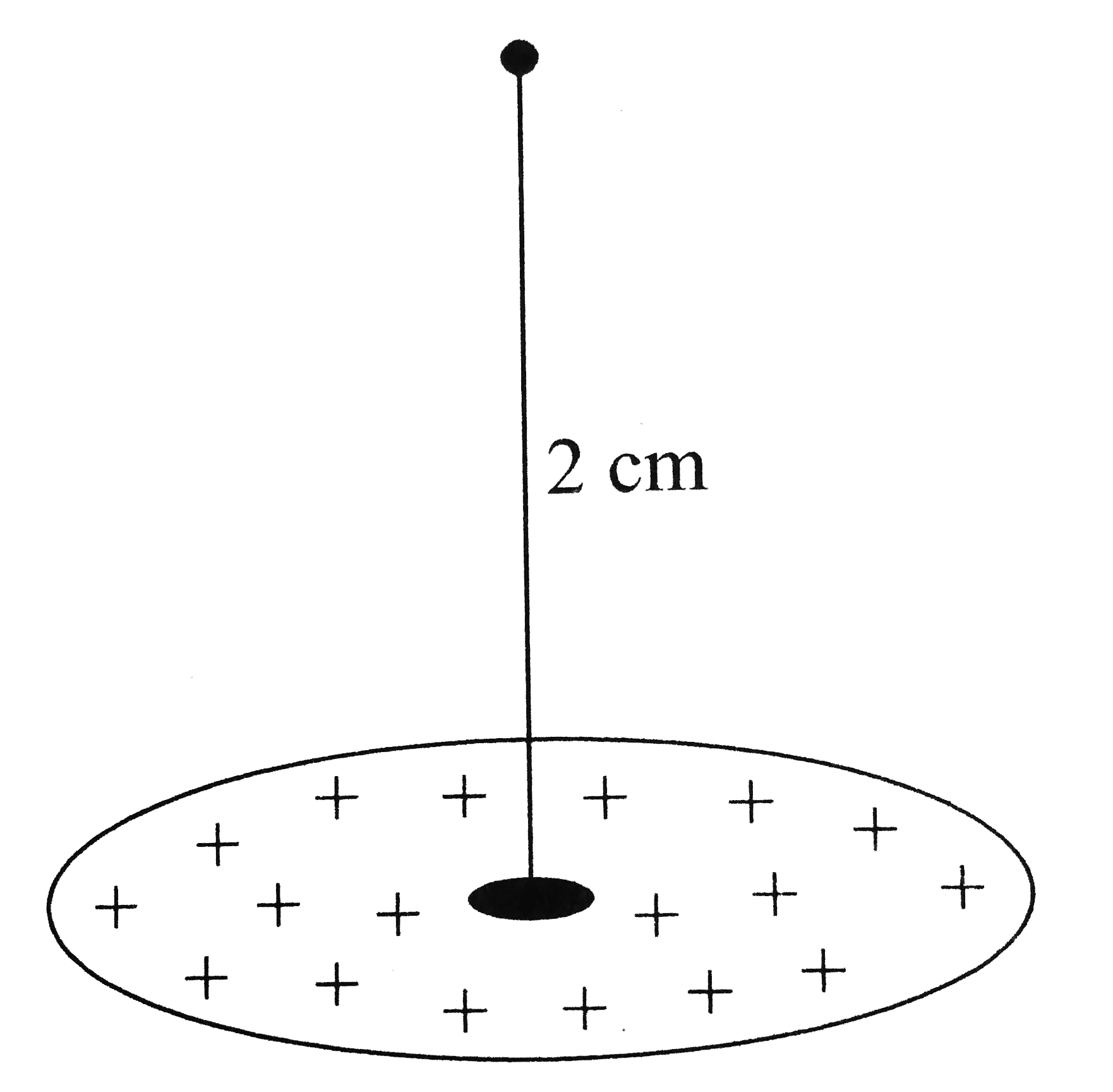
View SolutionA uniformly charged non conducting disc with surface charge density 10nC/m2 having radius R=3cm. Then find the value of electric field intensity at a point on the perpendicular bisector at a distance of r=2cm
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

View SolutionTwo uniformly charged non-conducting hemispherical shells each having uniform charge density σ and radius R from a complete sphere (not stuck together) and surround a concentric spherical conducting shell of radius R/2. If hemispherical parts are in equilibrium then minimum surface charge density of inner conducting shell is :
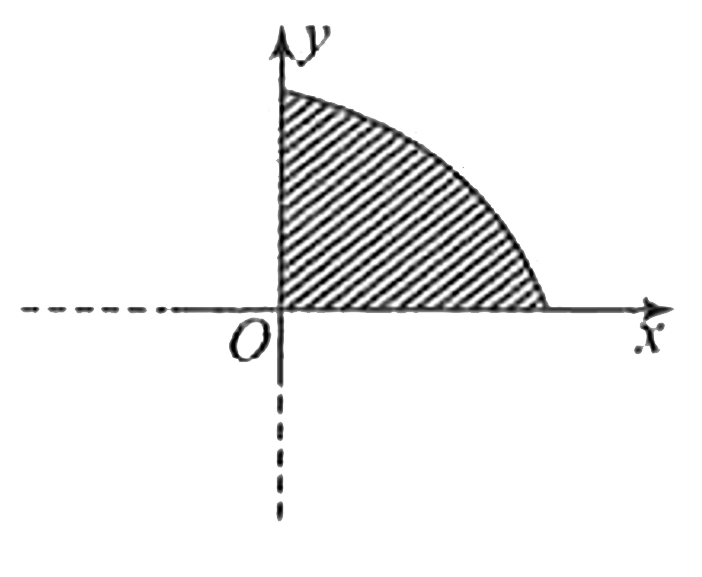
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
View Solution
