In a triangle ABC, ∠ABC=45∘ and a point D is on BC such that 2BD=CD and ∠DAB=15∘ then ∠ACB=
The correct Answer is:3
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have triangle ABC with:
- ∠ABC=45∘
- A point D on BC such that 2BD=CD
- ∠DAB=15∘
Step 2: Set up the triangle and angles
Let:
- ∠DAB=15∘
- ∠ABC=45∘
Since D divides BC in the ratio 2:1, we can denote:
- BD=x
- CD=2x
Step 3: Use the exterior angle theorem
According to the exterior angle theorem, we know that:
∠ADC=∠DAB+∠ABC
Substituting the known angles:
∠ADC=15∘+45∘=60∘
Step 4: Apply the MN theorem
Using the MN theorem, we have:
M+Ncotθ=NcotB+McotC
Where:
- M=2 (for CD)
- N=1 (for BD)
- θ=∠ADC=60∘
- B=∠ABC=45∘
- C=∠ACB
Substituting these values into the MN theorem:
2+1cot60∘=1⋅cot45∘+2⋅cotC
Step 5: Calculate cotangent values
We know:
- cot60∘=1√3
- cot45∘=1
Substituting these values:
31√3=1+2cotC
This simplifies to:
3√3=1+2cotC
Step 6: Solve for cotC
Rearranging the equation gives:
2cotC=3√3−1
Thus:
cotC=3√3−12
Step 7: Find angle C
To find C=∠ACB, we can find the angle corresponding to the cotangent:
cotC=2−√3
This corresponds to:
C=75∘
Final Answer
Thus, the angle ∠ACB is:
∠ACB=75∘
---
We have triangle ABC with:
- ∠ABC=45∘
- A point D on BC such that 2BD=CD
- ∠DAB=15∘
Let:
- ∠DAB=15∘
- ∠ABC=45∘
- BD=x
- CD=2x
According to the exterior angle theorem, we know that:
∠ADC=∠DAB+∠ABC
Substituting the known angles:
∠ADC=15∘+45∘=60∘
Using the MN theorem, we have:
M+Ncotθ=NcotB+McotC
Where:
- M=2 (for CD)
- N=1 (for BD)
- θ=∠ADC=60∘
- B=∠ABC=45∘
- C=∠ACB
2+1cot60∘=1⋅cot45∘+2⋅cotC
We know:
- cot60∘=1√3
- cot45∘=1
31√3=1+2cotC
This simplifies to:
3√3=1+2cotC
Rearranging the equation gives:
2cotC=3√3−1
Thus:
cotC=3√3−12
To find C=∠ACB, we can find the angle corresponding to the cotangent:
cotC=2−√3
This corresponds to:
C=75∘
Thus, the angle ∠ACB is:
∠ACB=75∘
Similar Questions
In triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn triangle ABC,AD=BD=CD (See figure). What is x?
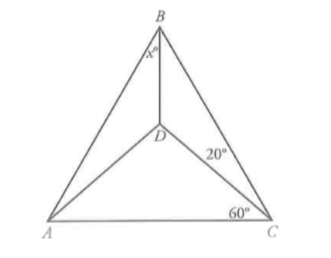 View Solution
View SolutionIn triangle ABC< D is on AC such that AD=BC and BD=DC, ∠DBC=2x and ∠BAD=3x where each angle is in degree. Then find x
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
 View Solution
View SolutionA Δ ABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionIn a right-angled triangle ABC,∠ABC=90∘ and D is mid-point of AC. Prove that BD=12AC.
View Solution

