A non-conducting wire is bent into a semi-circle of radius R and a charge +Q is uniformly distributed over it as shown in the figure. Find the ratio (VAEA) of the potential (VA) to the magnitude of the electric field (EA), both evaluated at the other end A of diameter AB that bisects the wire (as shown in the figure)
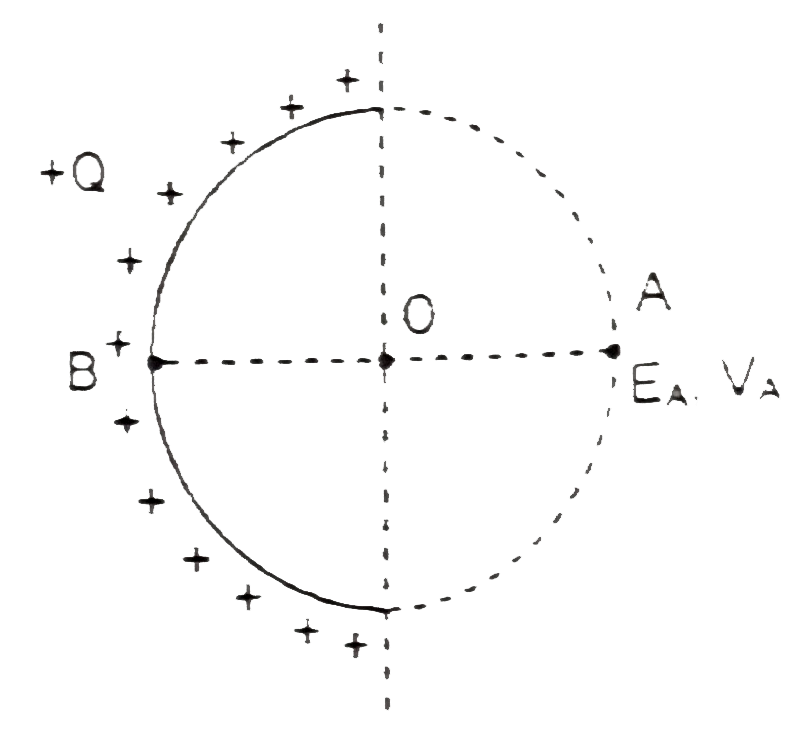
E=∫14πε0dqr2cosϕ, V=∫14πε0dqr, where r=2Rcosϕ

Similar Questions
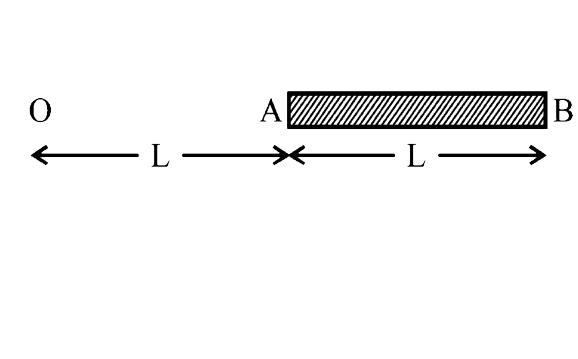
A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
 View Solution
View SolutionA charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
View SolutionA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge -Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is
 View Solution
View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionCharge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to
 View Solution
View SolutionInside a charged thin conducting shell of radius R, a point charge +Q is placed as shown in figure potential of shell may be
 View Solution
View SolutionA hemispherical surface of radius R is kept in a uniform electric field E as shown in figure. The flux through the curved surface is
 View Solution
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionFind out the flux through the curved surface of a hemisphere of radius R if it is placed in a uniform electric field E as shown in figure
 View Solution
View Solution

