A particle is projected up an inclined plane with initial speed 20 m/s at an angle 30∘ with the plane. Find the component of its velocity (in m/s) perpendicular to the plane, when it strikes the plane.
10√3m/s
10m/s
5√3m/s
data insufficient
The correct Answer is:B
Step by step video & image solution for A particle is projected up an inclined plane with initial speed 20 m/s at an angle 30^@ with the plane. Find the component of its velocity (in m/s) perpendicular to the plane, when it strikes the plane. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A particle is projected up an inclined plane with initial speed 20 m/s at an angle 30∘ with the plane. Find the component of its velocity (in m/s) perpendicular to the plane, when it strikes the plane.
View SolutionA particle is prjected up an inclined with initial speed v=20m/s at an angle θ=30∘ with the plane. The component of its velocity perpendicular to the plane when it strikes the plane is:
View SolutionIn the above problem, what is the component of its velocity perpendicular to the plane when it strikes at A ?
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA plane is inclined at an angle 30∘ with horizontal. The component of a vector →A=−10k perpendicular to this plane is: (here z-direction is vertically upwards)
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
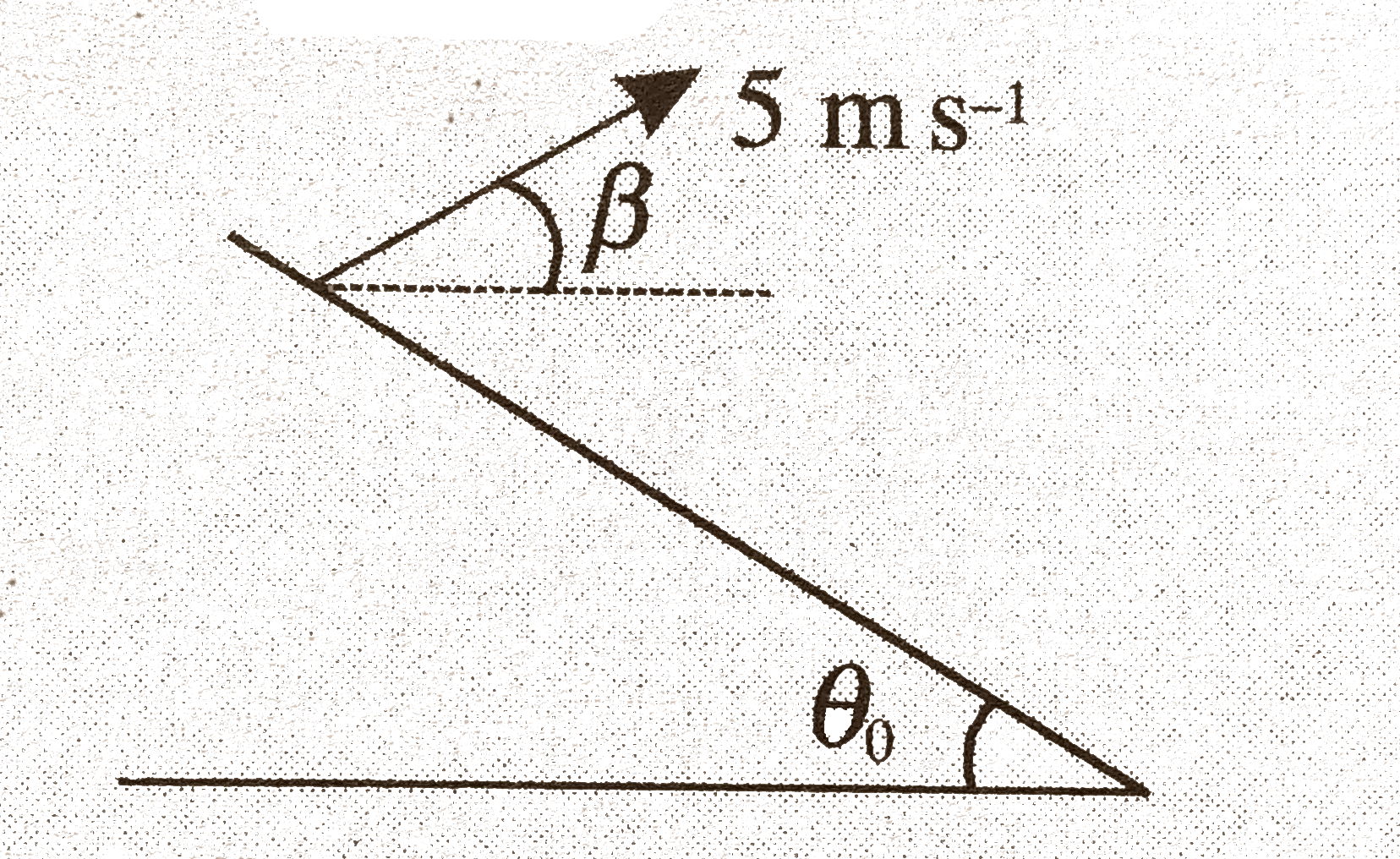 .
.
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View Solution
