A squre hole of side length l is made at a depth of h and a circular hole is made at a depht of 4 h from the surface of water in a water tank kept on a horizontal surface (where l ltlt h). Find the radius r of the circular hole if equal amount of water comes out of the vessel through the holes per second.
l/√2
l/2
l√π
l/√2π
The correct Answer is:D
To solve the problem of finding the radius r of the circular hole such that equal amounts of water flow out of both the square and circular holes per second, we can follow these steps:
Step 1: Identify the parameters
- Let the side length of the square hole be l.
- The depth of the square hole from the surface of the water is h.
- The depth of the circular hole from the surface of the water is 4h.
- The area of the square hole A1=l2.
- The area of the circular hole A2=πr2.
Step 2: Determine the efflux speed
According to Torricelli's theorem, the speed of efflux v of a fluid under gravity through a hole is given by:
v=√2gh
where g is the acceleration due to gravity and h is the depth of the hole from the surface of the fluid.
For the square hole at depth h:
v1=√2gh
For the circular hole at depth 4h:
v2=√2g(4h)=√8gh=2√2gh
Step 3: Set up the flow rate equation
The volume flow rate through each hole is given by:
Q1=A1v1=l2√2gh
Q2=A2v2=πr2(2√2gh)
Step 4: Equate the flow rates
Since the amount of water flowing out through both holes is the same, we can set Q1=Q2:
l2√2gh=πr2(2√2gh)
Step 5: Simplify the equation
We can cancel √2gh from both sides (assuming h≠0):
l2=2πr2
Step 6: Solve for r
Rearranging the equation gives:
r2=l22π
Taking the square root of both sides:
r=l√2π
Final Answer
Thus, the radius r of the circular hole is:
r=l√2π
---
- Let the side length of the square hole be l.
- The depth of the square hole from the surface of the water is h.
- The depth of the circular hole from the surface of the water is 4h.
- The area of the square hole A1=l2.
- The area of the circular hole A2=πr2.
According to Torricelli's theorem, the speed of efflux v of a fluid under gravity through a hole is given by:
v=√2gh
where g is the acceleration due to gravity and h is the depth of the hole from the surface of the fluid.
v1=√2gh
v2=√2g(4h)=√8gh=2√2gh
The volume flow rate through each hole is given by:
Q1=A1v1=l2√2gh
Q2=A2v2=πr2(2√2gh)
Since the amount of water flowing out through both holes is the same, we can set Q1=Q2:
l2√2gh=πr2(2√2gh)
We can cancel √2gh from both sides (assuming h≠0):
l2=2πr2
Rearranging the equation gives:
r2=l22π
Taking the square root of both sides:
r=l√2π
Thus, the radius r of the circular hole is:
r=l√2π
Similar Questions
A tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View Solution
Knowledge Check
A large open tank has two holes in the wall. One is square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth of 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then R is equal to
AL/√(2π)B2πLCLDL/2π
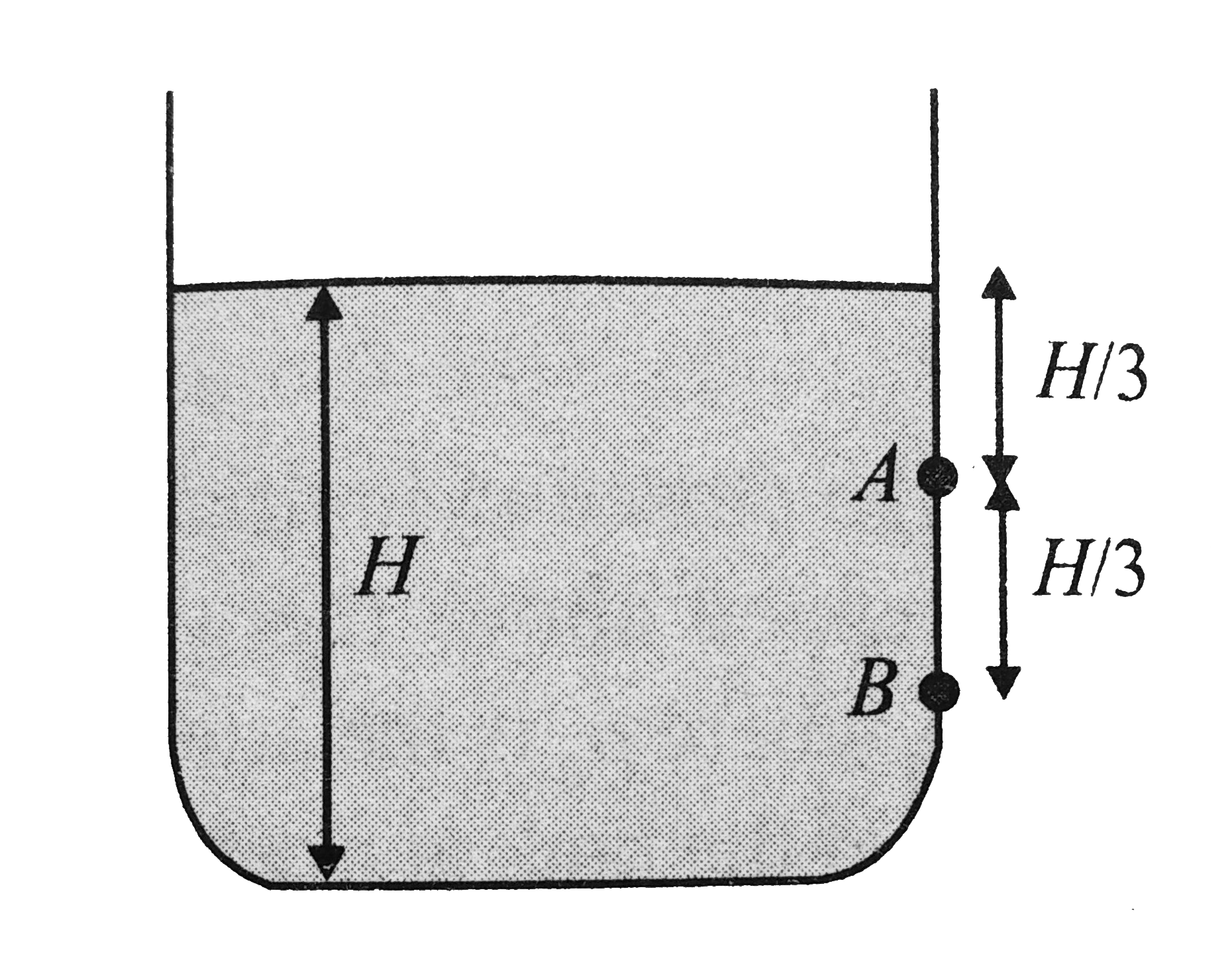
The area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
View SolutionA water tank has a hole at a distance of 7 m from free water surface. Find the velocity of water through the hole. If the radius of the hole is 2 mm what is the rate of flow of water?
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA tank of height H is fully filled with water. If the water rushing from a hole made in the tank below the free surface , strikes the floor at a maximum horizontal distance , then the depth of the hole from the free surface must be
View SolutionA small hollow sphere which has a small hole in it is immersed in water to a depth of 40 cm, before any water is penetrated into it. If the surface tensionof water si 0.073Nm−1, find the radius of the hole.
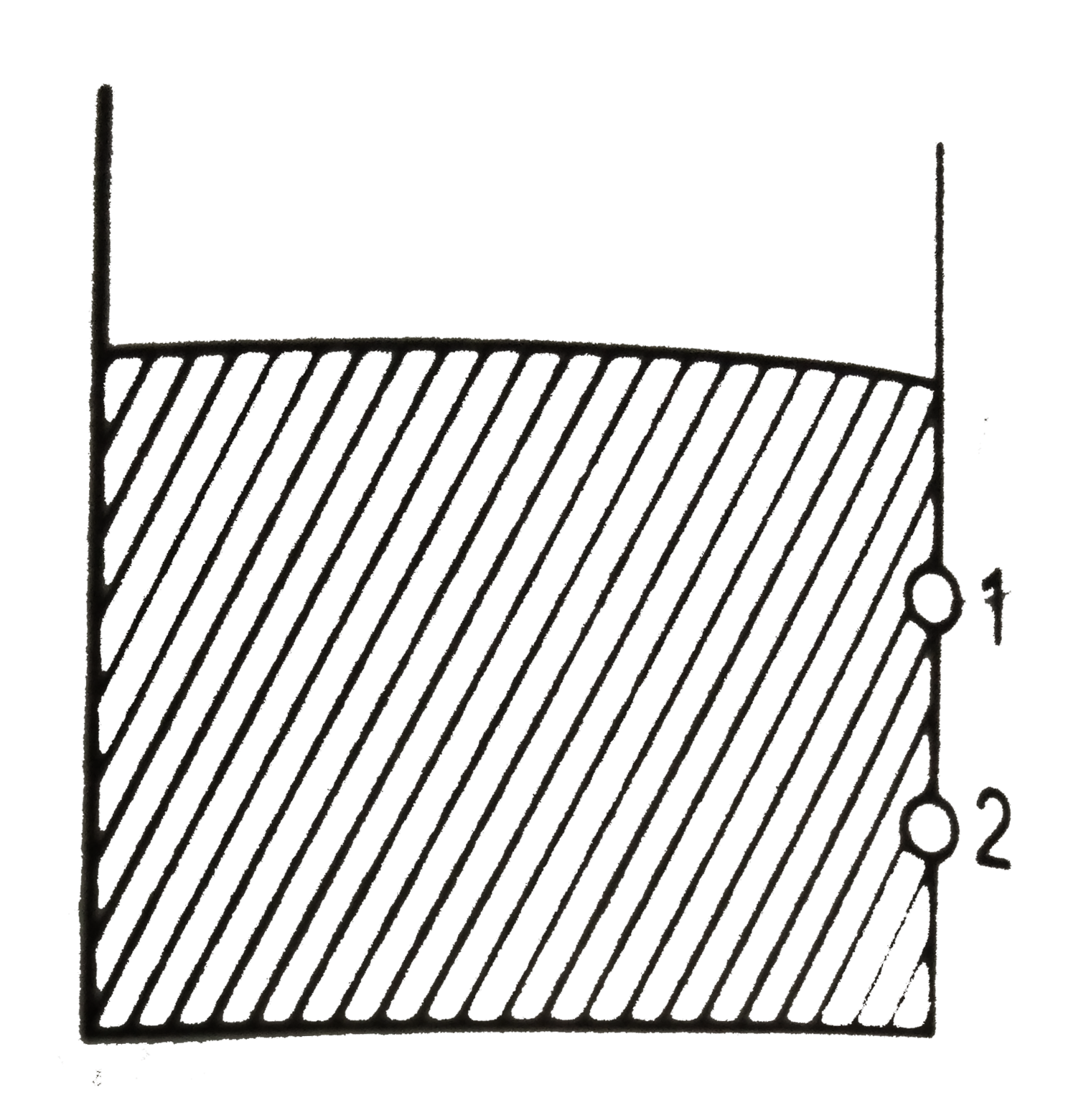
View SolutionTwo holes 1 and 2 are made at depths h and 16h reapectively. Both the holes are circular but radius of hole-1 is two times.
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View Solution
