Let V and E be the gravitational potential field. Then select the correct alternative (s)
the plot of E against r (distance from centre) is discontinuous for a spherical shell
the plot of V against r is continous for a spherical shell
the plot of E against r is discontinuous for a solid sphere
the plot of V against r is continuous for a solid sphere
The correct Answer is:A, B, D
To solve the question regarding the gravitational potential field V and the gravitational field E, we will analyze each statement provided in the question step by step.
Step 1: Analyze the first statement
Statement: The plot of E against R is discontinuous for the spherical shell.
- For a spherical shell, the gravitational field E inside the shell is zero, and outside the shell, it behaves like a point mass. Therefore, there is a discontinuity at the surface of the shell where the field jumps from 0 to a non-zero value.
- Conclusion: This statement is correct.
Step 2: Analyze the second statement
Statement: The plot of V against R is continuous for the spherical shell.
- The gravitational potential V inside the shell is constant (equal to the potential at the surface), and outside it decreases with 1/R. Since there is no jump in potential at the surface, the graph is continuous.
- Conclusion: This statement is correct.
Step 3: Analyze the third statement
Statement: The plot of E against R is discontinuous for the solid sphere.
- For a solid sphere, the gravitational field E inside the sphere varies linearly with R (proportional to R), and outside it behaves like a point mass (inversely proportional to R2). There is no discontinuity; the graph is continuous.
- Conclusion: This statement is incorrect.
Step 4: Analyze the fourth statement
Statement: The plot of V against R is continuous for a solid sphere.
- The gravitational potential V for a solid sphere is continuous. Inside the sphere, it increases linearly with R, and outside it decreases with 1/R. There is no discontinuity at the surface.
- Conclusion: This statement is correct.
Final Conclusion
Based on the analysis:
- The correct statements are: 1, 2, and 4.
Statement: The plot of E against R is discontinuous for the spherical shell.
- Conclusion: This statement is correct.
Statement: The plot of V against R is continuous for the spherical shell.
- Conclusion: This statement is correct.
Statement: The plot of E against R is discontinuous for the solid sphere.
- Conclusion: This statement is incorrect.
Statement: The plot of V against R is continuous for a solid sphere.
- Conclusion: This statement is correct.
Based on the analysis:
- The correct statements are: 1, 2, and 4.
Similar Questions
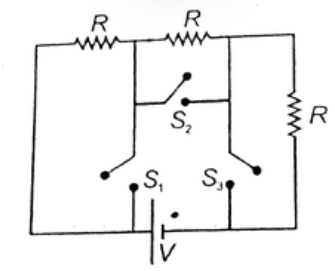
If all the resistors are identical , select the correct alternative (s).
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
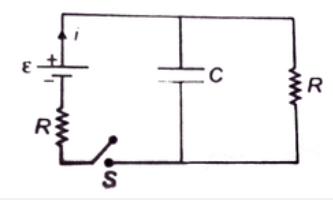
View SolutionIn the circuit shown, the switch is closed at t=0. Select the correct alternative(s)
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
View SolutionA particle moves in a straight line with constant acceleration under a constant force F. Select the correct alternative(s).
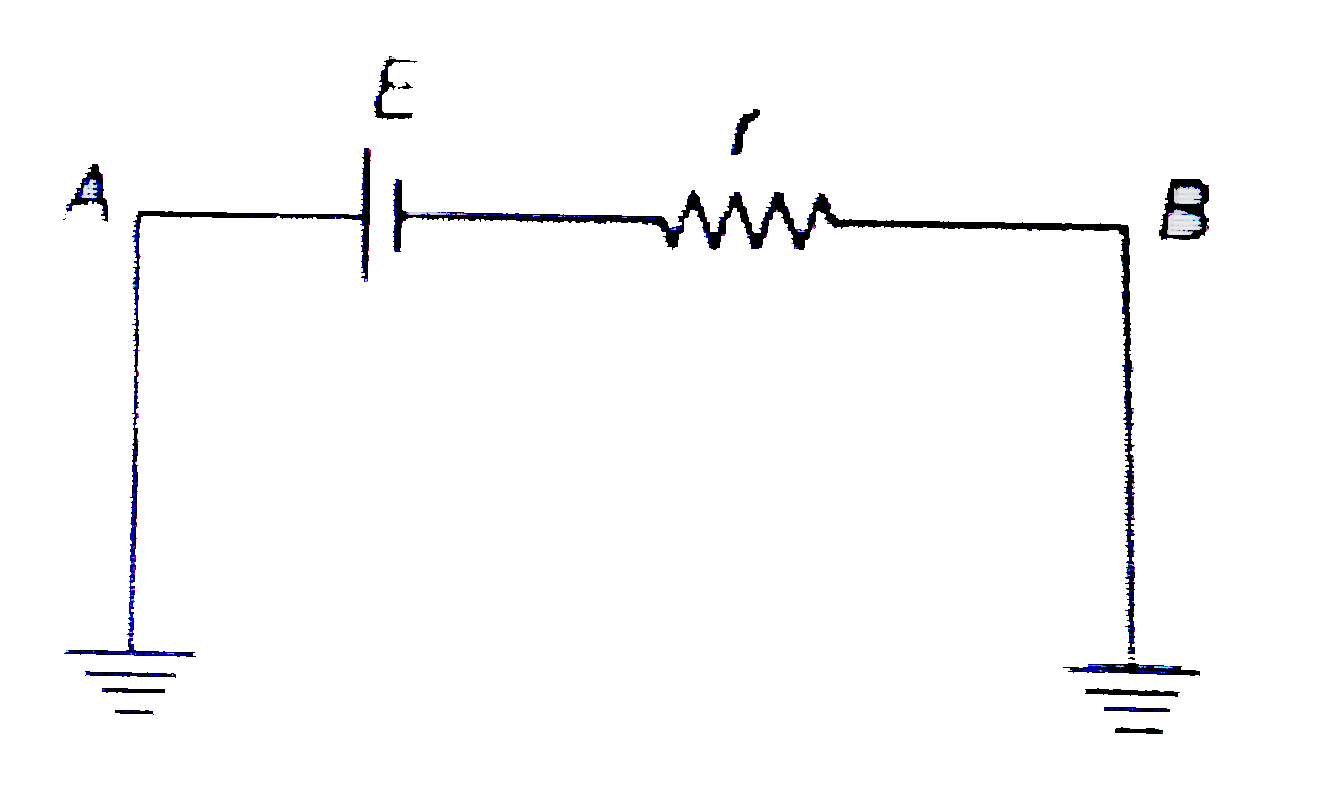
View SolutionBoth terminals of a battery of emf E and internal resistance r are grounded as shown. Select the correct alternative(s).
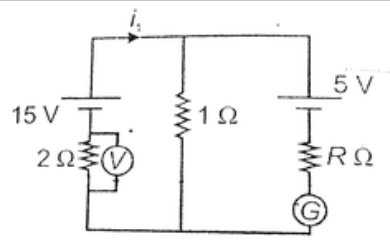
View SolutionIn the circuit shown, readint of galvanometer is zero. Select the correct alternative(s)
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
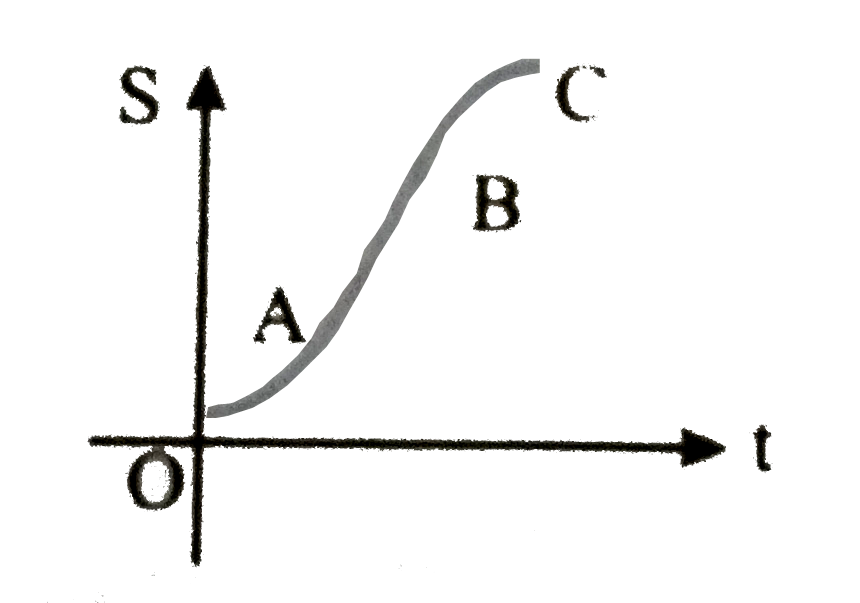 .
.
View SolutionA current enters from A and leaves at B through the network shown. Select the correct alternative(s).
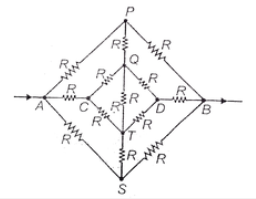
View Solution
