A particle moves in a straight line with constant acceleration under a constant force F. Select the correct alternative(s).
Power developed by this force varies linearly with time
Power developed by this force varies parabolically with time
Power developed by this force varies linearly with displacement
Power developed by this force varies parabolically with displacement
The correct Answer is:A, D
To solve the problem, we need to analyze the motion of a particle moving in a straight line with constant acceleration under a constant force F. We will derive the relationships between power, velocity, and displacement.
1. Understanding the Basics:
- A particle is moving with constant acceleration a under a constant force F.
- According to Newton's second law, F=ma, where m is the mass of the particle.
2. Power Definition:
- Power P is defined as the rate at which work is done or energy is transferred. Mathematically, it can be expressed as:
P=F⋅v
where v is the velocity of the particle.
3. Velocity Expression:
- From the equations of motion, the velocity v of the particle at time t can be expressed as:
v=u+at
where u is the initial velocity.
4. Substituting Velocity into Power:
- Substituting the expression for v into the power equation gives:
P=F⋅(u+at)
- This shows that power is directly proportional to time t since F and u are constants.
5. Displacement Expression:
- Another equation of motion relates displacement s to time:
s=ut+12at2
6. Finding Power in Terms of Displacement:
- From the equation v2=u2+2as, we can express v in terms of displacement:
v=√u2+2as
- Substituting this into the power equation gives:
P=F⋅√u2+2as
7. Analyzing Power with Displacement:
- As s increases, P will vary as the square root of s. Therefore, we can say:
P2∝s
- This indicates that power varies parabolically with displacement s.
Conclusion:
- The correct alternatives are:
- Power developed by this force varies linearly with time.
- Power developed by this force varies parabolically with displacement.
- A particle is moving with constant acceleration a under a constant force F.
- According to Newton's second law, F=ma, where m is the mass of the particle.
- Power P is defined as the rate at which work is done or energy is transferred. Mathematically, it can be expressed as:
P=F⋅v
where v is the velocity of the particle.
- From the equations of motion, the velocity v of the particle at time t can be expressed as:
v=u+at
where u is the initial velocity.
- Substituting the expression for v into the power equation gives:
P=F⋅(u+at)
- This shows that power is directly proportional to time t since F and u are constants.
- Another equation of motion relates displacement s to time:
s=ut+12at2
- From the equation v2=u2+2as, we can express v in terms of displacement:
v=√u2+2as
- Substituting this into the power equation gives:
P=F⋅√u2+2as
- As s increases, P will vary as the square root of s. Therefore, we can say:
P2∝s
- This indicates that power varies parabolically with displacement s.
- The correct alternatives are:
- Power developed by this force varies linearly with time.
- Power developed by this force varies parabolically with displacement.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions
10 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionStatement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
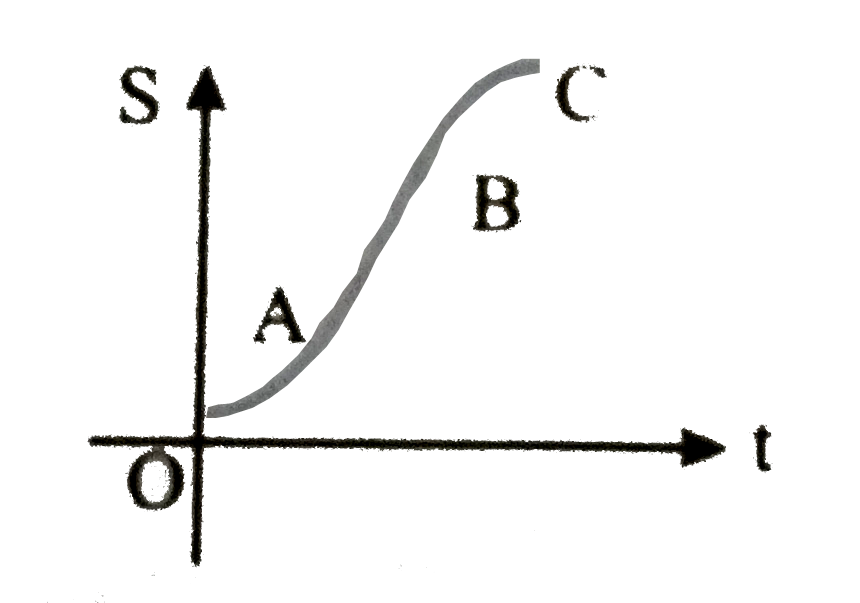 .
.
View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and tenth second it travels a distance od 10m. Then the acceleration of the particle will be.
View SolutionA particle moves in a straight line so that s=√t, then its acceleration is proportional to
View SolutionA particle moves in a straight line so that s=√t, then its acceleration is proportional to
View Solution
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive
View SolutionA particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View Solution
