Obtain an expression for electric potential at a distance r from isolated positive charge.
Consider a charge +q placed at point O. In order to calculate the potential at point P, let OP=r. Let a positive charge q0 be placed at point A. The electric field intensity at point A is given by
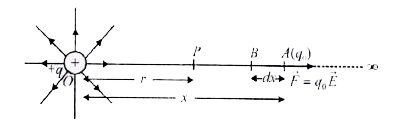
E=14πε0qx2........(i)
This electric field exerts a force on charge q0 which is given by
→F=q0→E............(ii)
This force acts radially outwards.
The work done to move q0 from A to B is given by
dW=→F⋅d→x
The force →F and displacement d→x are opposite to each other i.e. θ=180∘.
So, dW=q0→Ed→x=q0Edxcos180∘=−q0Edx [using equation (ii)]
or dW=−14πε0=qq0x2dx..............(iii) [using equation (i)]
Where E=14πε0qx2
Total work done to move q0 from infinity (x=∞) to point P(x=r) against electric field is given by
WP=∫P∞dW or WP=∫x=rx=0o−14πε0qq0x2dx=−qq04πε0[−1x]x=rx=∞
or WP=qq04πε0[1r−1∞]=qq04πε0[1r−0] or WP=14πε0qq0r.
or, WPq0=14πε0qr.............(iv)
From the definition of electric potential, we know that
Electric potential V=WPq0 .............(v)
From equation (iv) and (v), we have V=14πε0qr.
Similar Questions
Knowledge Check
The dependence of electric potential V on the distance 'r' from the centre of a charged spherical shell is shown by :
A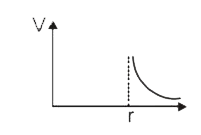 B
B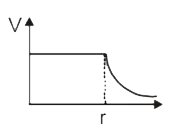 C
C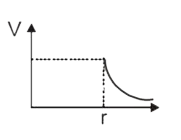 D
D
Which graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?
A
 B
B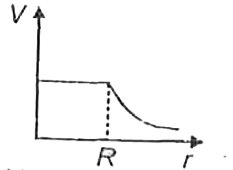 C
C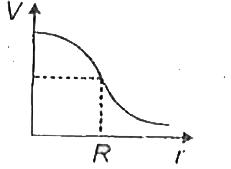 D
D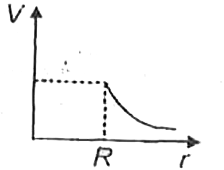
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
AWQxBWCWxDWQ
If V and u are electric potential and energy density, respectively, at a distance r from a positive point charge, then which of the following graph is correct ?
View SolutionIf V and u are electric potential and energy density, respectively, at a distance r from a positive point charge, then which of the following graph is correct ?
View SolutionA positive point charge is released from rest at a distance r0 from a positive line charge with uniform density. The speed (v) of the point charge, as a function of instantaneous distance r from line charge, is proportional to:

View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.
View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.
View Solution
