Question

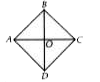
If ABCD be a rhombus, AC is its smallest diagonal and $\angle ABC={60}^{\circ }$, find length of a side of the rhombus when $AC=6cm$.

Options

A. `6 cm.`
B. `3 cm`.
C. `6sqrt(2) cm`
D. `3sqrt(3) cm.`

Answer

A

Explanation

To find the length of a side of the rhombus ABCD, given that AC is the smallest diagonal and measures 6 cm, and the angle ∠ABC = 60°, we can follow these steps:

Step 1: Understand the properties of a rhombus
A rhombus has all sides equal, and its diagonals bisect each other at right angles. The diagonals also bisect the angles of the rhombus.

Step 2: Identify the diagonals
Let AC be the smallest diagonal, which is given as 6 cm. Since diagonals bisect each other, we can denote the midpoint of AC as O. Therefore, AO = OC = 6 cm / 2 = 3 cm.

Step 3: Determine the angles
Since ∠ABC = 60°, and diagonals bisect the angles, we have:
- ∠AOB = ∠COD = 60° (since diagonals bisect the angles)
- Therefore, ∠AOB = 60° implies that ∠AOC = 120° (because the sum of angles around point O is 360°, and the diagonals bisect each other).

Step 4: Use the properties of triangles
In triangle AOB, we can use the sine rule or cosine rule to find the length of side AB. Since we have:
- AO = 3 cm (half of diagonal AC)
- ∠AOB = 60°

Using the cosine rule in triangle AOB:
\( AB^2 = AO^2 + OB^2 - 2 \cdot AO \cdot OB \cdot \cos(\angle AOB) \)

Since AO = OB (because diagonals bisect each other), let AB = s (the side of the rhombus):
\( s^2 = 3^2 + 3^2 - 2 \cdot 3 \cdot 3 \cdot \cos(60°) \)

Step 5: Calculate using cosine value
We know that:
- \(\cos(60°) = \frac{1}{2}\)

Substituting this into the equation:
\( s^2 = 9 + 9 - 2 \cdot 3 \cdot 3 \cdot \frac{1}{2} \)
\( s^2 = 9 + 9 - 9 \)
\( s^2 = 9 \)

Step 6: Find the length of the side
Taking the square root of both sides:
\( s = \sqrt{9} = 3 \text{ cm} \)

Thus, the length of a side of the rhombus is 3 cm.