ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?

A

$E D > C F$

B

$E D_{I}_C F$

C

$E D^{2} + C F^{2} = E F^{2}$

D

$E D ∣ ∣ C F$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

|

Answer

Step by step video, text & image solution for ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
A $E D^{2} + C F^{2} = E F^{2}$
B $E D / C F$
C $E D > C F$
D $E D 1 C F$
Question 2 - Select One
ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
A $E D > C F$
B $E D_{I}_C F$
C $E D^{2} + C F^{2} = E F^{2}$
D $E D ∣ ∣ C F$
Question 3 - Select One
In the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.

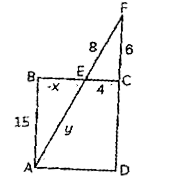
Perimeter of $Δ A B E =$
A35cm
B36cm
C40cm
D45cm

KIRAN PUBLICATION-GEOMETRY-QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)

Home
Ask Doubt
Profile