ABCD is a cyclic trapezium with AD∣∣BC, If ∠A=105∘, then other three angles are
∠B=75∘,∠C=75∘,∠D=105∘
∠B=105∘,∠C=75∘,∠D=75∘
∠B=75∘,∠C=105∘,∠D=75∘
∠B=105∘,∠C=105∘,∠D=75∘
The correct Answer is:A
To solve the problem, we need to find the angles B, C, and D of the cyclic trapezium ABCD, given that angle A is 105 degrees and that AD is parallel to BC.
1. Identify the given information:
- We know that ABCD is a cyclic trapezium with AD || BC.
- Given angle A = 105 degrees.
2. Use the property of cyclic trapeziums:
- In a cyclic trapezium, the sum of the opposite angles is 180 degrees. Therefore, we can write:
∠A+∠C=180∘
- Substituting the value of angle A:
105∘+∠C=180∘
3. Solve for angle C:
- Rearranging the equation gives:
∠C=180∘−105∘=75∘
4. Use the property of parallel lines:
- Since AD is parallel to BC, by the properties of interior angles formed by a transversal, we have:
∠A+∠B=180∘
- Substituting the value of angle A:
105∘+∠B=180∘
5. Solve for angle B:
- Rearranging the equation gives:
∠B=180∘−105∘=75∘
6. Find angle D using the cyclic trapezium property:
- Again, using the property of opposite angles:
∠B+∠D=180∘
- Substituting the value of angle B:
75∘+∠D=180∘
7. Solve for angle D:
- Rearranging the equation gives:
∠D=180∘−75∘=105∘
Summary of Angles:
- Angle A = 105 degrees
- Angle B = 75 degrees
- Angle C = 75 degrees
- Angle D = 105 degrees
Final Answer:
- Angles B, C, and D are 75 degrees, 75 degrees, and 105 degrees respectively.
- We know that ABCD is a cyclic trapezium with AD || BC.
- Given angle A = 105 degrees.
- In a cyclic trapezium, the sum of the opposite angles is 180 degrees. Therefore, we can write:
∠A+∠C=180∘
- Substituting the value of angle A:
105∘+∠C=180∘
- Rearranging the equation gives:
∠C=180∘−105∘=75∘
- Since AD is parallel to BC, by the properties of interior angles formed by a transversal, we have:
∠A+∠B=180∘
- Substituting the value of angle A:
105∘+∠B=180∘
- Rearranging the equation gives:
∠B=180∘−105∘=75∘
- Again, using the property of opposite angles:
∠B+∠D=180∘
- Substituting the value of angle B:
75∘+∠D=180∘
- Rearranging the equation gives:
∠D=180∘−75∘=105∘
- Angle A = 105 degrees
- Angle B = 75 degrees
- Angle C = 75 degrees
- Angle D = 105 degrees
- Angles B, C, and D are 75 degrees, 75 degrees, and 105 degrees respectively.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)70videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- X)25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a cyclic trapezium such that AD || BC. If ∠ABC=70∘, then the value of ∠BCD is :
A60∘B70∘C40∘D80∘ - Question 2 - Select One
ABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
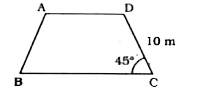 A10√2mB4√2mC5√2mD6√2m
A10√2mB4√2mC5√2mD6√2m - Question 3 - Select One
ABCD is a cyclic trapezium whose side AD and BC are parallel to each other. If ∠ABC=62∘ then the measure of the ∠BCD is :
A120∘B118∘C62∘D28∘
ABCD is a cyclic trapezium in which, AD| |BC and ∠B=70∘. Find its remaining angles,
View SolutionABCD is a cyclic quadrilateral. If AD∣∣BCand∠B=70∘, find the other angles of ABCD.
View SolutionIn trapezium ABCD with AB||CD, if ∠A=100°, then ∠D= __________.
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠C=∠D
 View Solution
View SolutionABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC=72∘, then the measure of the ∠BCD is
View Solution

