If a chord of a circle of radius 5 cm is a tangent to another circle of radius 3 cm, both the circles being concentric, then the length of the chord is
10 cm
12.5 cm
8 cm
7 cm
The correct Answer is:C
To solve the problem, we need to find the length of the chord of a circle with a radius of 5 cm, which is tangent to another concentric circle with a radius of 3 cm.
1. Understand the Geometry:
We have two concentric circles. The larger circle has a radius of 5 cm, and the smaller circle has a radius of 3 cm. The chord of the larger circle is tangent to the smaller circle.
2. Draw the Diagram:
Draw two concentric circles. Label the center as O. The larger circle (radius 5 cm) and the smaller circle (radius 3 cm) should be clearly marked.
3. Identify the Tangent Point:
Let the point where the chord touches the smaller circle be point T. Since the chord is tangent to the smaller circle, the distance from the center O to the point T is equal to the radius of the smaller circle, which is 3 cm.
4. Draw the Perpendicular from the Center to the Chord:
Draw a perpendicular line from the center O to the chord. Let the point where this perpendicular meets the chord be point M. This line OM bisects the chord.
5. Use the Pythagorean Theorem:
In the right triangle OMT:
- OM is the distance from the center to the chord (which is 3 cm).
- OT is the radius of the larger circle (which is 5 cm).
- MT is half the length of the chord (let's denote it as x).
According to the Pythagorean theorem:
OT2=OM2+MT2
Substituting the known values:
52=32+x2
25=9+x2
x2=25−9
x2=16
x=4
6. Calculate the Length of the Chord:
Since MT is half the length of the chord, the full length of the chord (let's denote it as L) is:
L=2×MT=2×4=8 cm
Final Answer:
The length of the chord is 8 cm.
We have two concentric circles. The larger circle has a radius of 5 cm, and the smaller circle has a radius of 3 cm. The chord of the larger circle is tangent to the smaller circle.
Draw two concentric circles. Label the center as O. The larger circle (radius 5 cm) and the smaller circle (radius 3 cm) should be clearly marked.
Let the point where the chord touches the smaller circle be point T. Since the chord is tangent to the smaller circle, the distance from the center O to the point T is equal to the radius of the smaller circle, which is 3 cm.
Draw a perpendicular line from the center O to the chord. Let the point where this perpendicular meets the chord be point M. This line OM bisects the chord.
In the right triangle OMT:
- OM is the distance from the center to the chord (which is 3 cm).
- OT is the radius of the larger circle (which is 5 cm).
- MT is half the length of the chord (let's denote it as x).
OT2=OM2+MT2
Substituting the known values:
52=32+x2
25=9+x2
x2=25−9
x2=16
x=4
Since MT is half the length of the chord, the full length of the chord (let's denote it as L) is:
L=2×MT=2×4=8 cm
The length of the chord is 8 cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
The chord of circle whose radius is 5 cm touches another circle radius is 3 cm. If two circles are concentric, then what is length of chord?
Aa)10 cmBb)12.5 cmCc)8 cmDd)7 cm - Question 2 - Select One
EF is a chord of a circle whose length is 10 cm. If radius of the circle is 13 cm, then the length of perpendicular from the centre to the chord is
A12 cmB8 cmC7 cmD5 cm - Question 3 - Select One
In the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
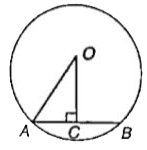 A35 cmB30 cmC15 cmD18 cm
A35 cmB30 cmC15 cmD18 cm
The chord of a circle of radius 10cm subtends a right angle at its centre. The length of the chord (in cm) is
View SolutionPQ is chord of length 6 cm of a circle of radius 5 cm. Tangents to the circle at P and Q meet at T. Length of TP is
View SolutionA chord of a circle is equal to its radius. A tangent is drawn to the circle at an extremity of the chord. The angle between the tangent and the chord is
View SolutionIn a circle of radius 10 cm, a chord is at a distance of 6 cm from the centre. The length of chord is
View SolutionFrom the centre of a circle, distance of a chord is 16 cm. If radius of the circle be 20 cm. What will be the length of the chord?
View Solution

