Two circles Intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the tangents PT and PQ drawn from point P to the two circles that intersect at points A and B.
1. Identify the Elements:
- Let the two circles intersect at points A and B.
- Point P is on the line extended from segment AB.
- PT is a tangent to one circle from point P.
- PQ is a tangent to the other circle from point P.
2. Use the Tangent-Secant Theorem:
- According to the tangent-secant theorem, if a tangent is drawn from a point outside a circle, the square of the length of the tangent segment is equal to the product of the lengths of the whole secant segment and its external part.
- For the first circle, we have:
PT2=PA⋅PB
- For the second circle, we have:
PQ2=PA⋅PB
3. Set the Equations Equal:
- Since both PT and PQ are tangents from point P to their respective circles, we can equate the two equations:
PT2=PQ2
4. Conclude the Relationship:
- Taking the square root of both sides gives us:
PT=PQ
- This means that the lengths of the tangents PT and PQ are equal.
Final Answer:
The relation between the tangents PT and PQ is:
PT=PQ
- Let the two circles intersect at points A and B.
- Point P is on the line extended from segment AB.
- PT is a tangent to one circle from point P.
- PQ is a tangent to the other circle from point P.
- According to the tangent-secant theorem, if a tangent is drawn from a point outside a circle, the square of the length of the tangent segment is equal to the product of the lengths of the whole secant segment and its external part.
- For the first circle, we have:
PT2=PA⋅PB
- For the second circle, we have:
PQ2=PA⋅PB
- Since both PT and PQ are tangents from point P to their respective circles, we can equate the two equations:
PT2=PQ2
- Taking the square root of both sides gives us:
PT=PQ
- This means that the lengths of the tangents PT and PQ are equal.
The relation between the tangents PT and PQ is:
PT=PQ
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
As per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
View SolutionTwo circles with centers O and O' of radii 6cm and 8 cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle. The length of the common chord PQ is
View Solution
Knowledge Check
Two circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
A45∘B90∘C80∘D100∘
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm , respectively intersect at two points P and Q such that OP and O'P are tangents to the two circle . Find the length of the common chord PQ.
View SolutionTwo circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
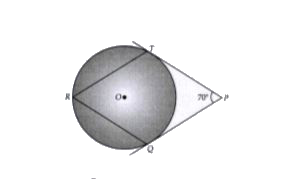
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
View SolutionPQ and RS are common tangents of two circles intersection at A and B. AB, when produced both sides, meet the tangents PQ and RS at x and y, respectively. If AB = 3 cm, xy = 5 cm, then PQ (in cm) will be.
View SolutionIn the figure, PT, PR and BA are the tangents to the circle. If ∠BPA=70∘, then the value of ∠AOB is
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

View Solution
