From an external point two tangents to a circle are drawn. The chord passing through the points of contact subtends an angle 72∘ at the centre. The angle between the tangents is
36∘
72∘
108∘
144∘
The correct Answer is:C
To find the angle between the two tangents drawn from an external point to a circle, we can follow these steps:
1. Identify the given information:
- Let the circle have center O.
- Let the external point from which the tangents are drawn be P.
- The points of contact on the circle are A and B.
- The angle subtended by the chord AB at the center O is given as 72°.
2. Understand the properties of tangents:
- The radius at the point of contact is perpendicular to the tangent. Therefore, OA ⊥ PA and OB ⊥ PB.
- This means that angles OAP and OBP are both 90°.
3. Create a quadrilateral:
- Consider the quadrilateral OAPB formed by the center O, the external point P, and the points of contact A and B.
4. Calculate the angles in the quadrilateral:
- The sum of the angles in a quadrilateral is 360°.
- We have:
- Angle OAP = 90°
- Angle OBP = 90°
- Angle AOB = 72° (given)
5. Set up the equation:
- Let the angle between the tangents PA and PB be denoted as ∠APB.
- According to the property of quadrilaterals:
∠OAP+∠OBP+∠AOB+∠APB=360°
- Substituting the known values:
90°+90°+72°+∠APB=360°
6. Simplify the equation:
- Combine the known angles:
180°+72°+∠APB=360°
- This simplifies to:
252°+∠APB=360°
7. Solve for ∠APB:
- Rearranging gives:
∠APB=360°−252°=108°
8. Conclusion:
- The angle between the tangents PA and PB is 108°.
Final Answer:
The angle between the tangents is 108°.
---
- Let the circle have center O.
- Let the external point from which the tangents are drawn be P.
- The points of contact on the circle are A and B.
- The angle subtended by the chord AB at the center O is given as 72°.
- The radius at the point of contact is perpendicular to the tangent. Therefore, OA ⊥ PA and OB ⊥ PB.
- This means that angles OAP and OBP are both 90°.
- Consider the quadrilateral OAPB formed by the center O, the external point P, and the points of contact A and B.
- The sum of the angles in a quadrilateral is 360°.
- We have:
- Angle OAP = 90°
- Angle OBP = 90°
- Angle AOB = 72° (given)
- Let the angle between the tangents PA and PB be denoted as ∠APB.
- According to the property of quadrilaterals:
∠OAP+∠OBP+∠AOB+∠APB=360°
- Substituting the known values:
90°+90°+72°+∠APB=360°
- Combine the known angles:
180°+72°+∠APB=360°
- This simplifies to:
252°+∠APB=360°
- Rearranging gives:
∠APB=360°−252°=108°
- The angle between the tangents PA and PB is 108°.
The angle between the tangents is 108°.
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
In From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
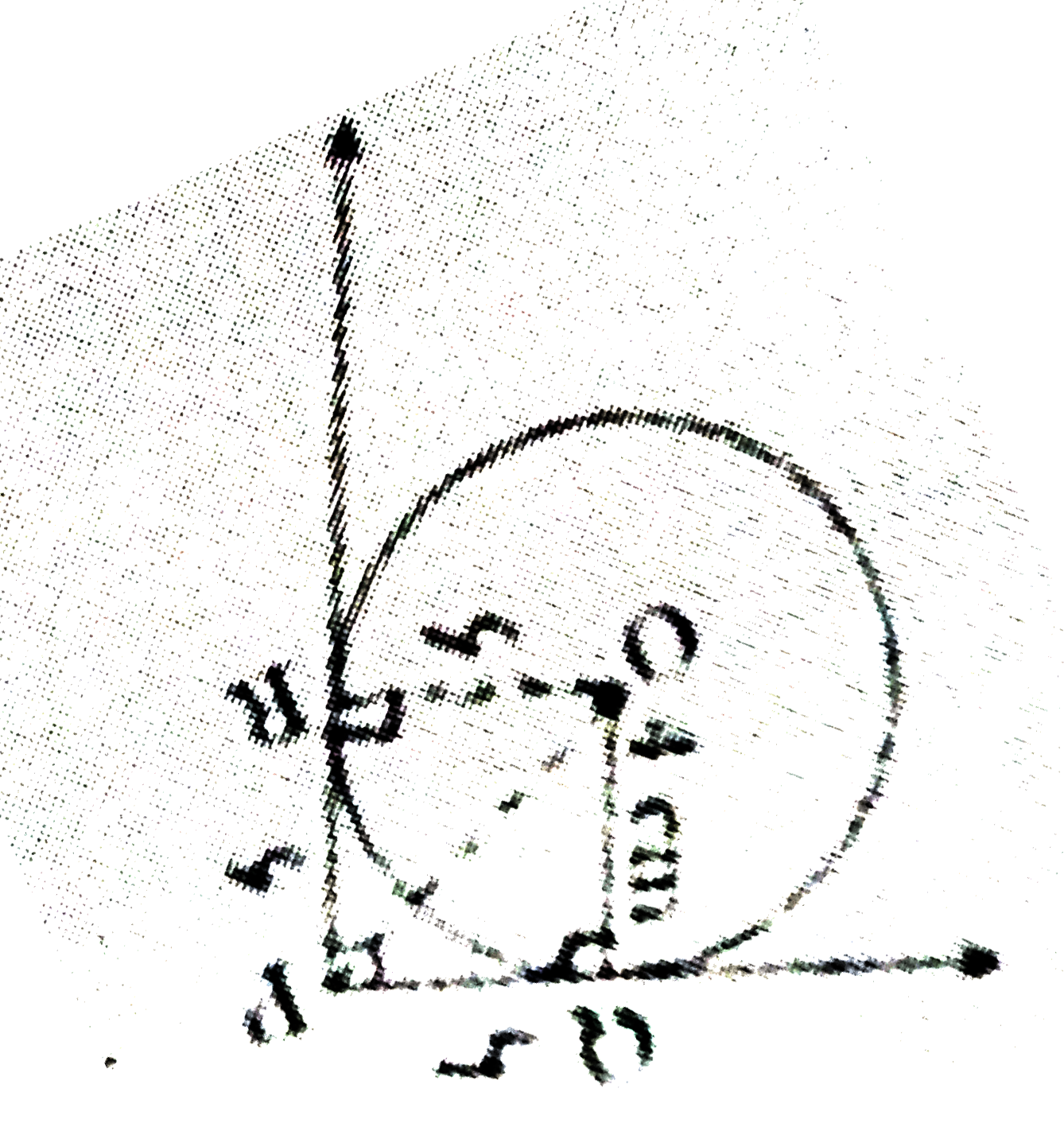
View SolutionIf we draw a tangents to a circle at a given point on it, when the centre of the circle is known, then the angle between the tangent and radius of the circle is
View Solution
Knowledge Check
2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
A24 cm.B6 cm.C8 cm.DCannot be determinedChoose the CORRECT option about the two tangents drawn to the circle from the external point?
1. The tangents subtend equal angles at the centre of the circle.
2. The tangents drawn from the external point to a circle are equal in length.
3. The tangents are equally inclined to the segment which joins the centre to that point.A1 and 2 onlyB2 and 3 onlyC1, 2 and 3D1 and 3 onlyIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is :
Aπ4Bπ3Cπ2Dπ6
Theorem:If two tangents are drawn to a circle from an external point ; then (i) they subtend equal angles at the centre. (ii) they are equally inclined to the line segments ; joining the centre to that point.
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionFrom the external point P tangents PA and PB are drawn to a circle with centre O. If ∠PAB=50∘, then find ∠AOB.
View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View Solution5. The locus of point of intersection of two tangents to the parabola y2=4x such that their chord of contact subtends a right angle at the vertex is
View Solution
