A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
78∘
96∘
102∘
108∘
The correct Answer is:D
To find the value of angle ∠AOB, we will follow these steps:
Step 1: Identify the angles in triangle ACT
We know:
- ∠ATC=30∘
- ∠ACT=48∘
Using the triangle sum property, we can find ∠CAT:
∠CAT=180∘−∠ATC−∠ACT
Substituting the values:
∠CAT=180∘−30∘−48∘=102∘
Step 2: Relate angles with the center O
Since OC is a radius and CT is a tangent at point C, we know that:
∠OCA=90∘
Now, we can find ∠OAC:
∠OAC=90∘−∠ACT=90∘−48∘=42∘
Step 3: Find angle AOB
In triangle OAC, we have:
- ∠OAC=42∘
- ∠OCA=90∘
Using the triangle sum property again:
∠AOC=180∘−∠OAC−∠OCA
Substituting the values:
∠AOC=180∘−42∘−90∘=48∘
Step 4: Relate ∠AOB with ∠AOC
Since O is the center of the circle, the angle ∠AOB is twice the angle ∠ACB (the angle subtended by the same arc):
∠AOB=2×∠AOC=2×48∘=96∘
Final Answer
Thus, the value of ∠AOB is:
∠AOB=96∘
---
We know:
- ∠ATC=30∘
- ∠ACT=48∘
∠CAT=180∘−∠ATC−∠ACT
Substituting the values:
∠CAT=180∘−30∘−48∘=102∘
Since OC is a radius and CT is a tangent at point C, we know that:
∠OCA=90∘
Now, we can find ∠OAC:
∠OAC=90∘−∠ACT=90∘−48∘=42∘
In triangle OAC, we have:
- ∠OAC=42∘
- ∠OCA=90∘
∠AOC=180∘−∠OAC−∠OCA
Substituting the values:
∠AOC=180∘−42∘−90∘=48∘
Since O is the center of the circle, the angle ∠AOB is twice the angle ∠ACB (the angle subtended by the same arc):
∠AOB=2×∠AOC=2×48∘=96∘
Thus, the value of ∠AOB is:
∠AOB=96∘
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
AB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB ?
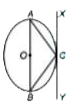
View Solution
Knowledge Check
AB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
A56∘B34∘C68∘D124∘A, B and C are three points on a circle. The tangent at C meets BA extended at T. Given, ∠ATC=36∘and∠ACT=48∘, the angle subtended by AB at the centre of the circle is
A84∘B48∘C96∘D72∘AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?A5∘B7∘C17∘D6∘
In the figure given below (not drawn to scale), A, B and C are three points on a circle with centre O. The chord BA is extended to a point T such that CT becomes a tangent to the circle at point C. If ∠ATC=30∘and∠ACT=50∘, then the angle ∠BOA is :

View SolutionA, B, C are three point on a circle. The tangent at A meets BC produced at T,∠BTA=40∘,∠CAT=44∘ . The angle subtended by BC at the centre of the circle is -
View SolutionΔABCis inscribed in a circle so that BC is diameter. The tangent at a point C intersects BA when produced at a point D. If ∠ABC=36∘ then the value of ∠ADCis
View SolutionLet P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with ∠PAQ=48∘, then ∠APQ is
View SolutionIn the given figure, O is the centre of the circle, ∠CAO = 35∘ and ∠CBO= 45∘. What is the value (In degrees) of ∠AOB?
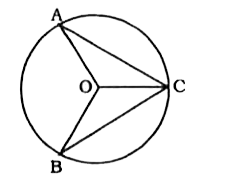
View Solution
