ABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
Given two ΔABCandΔDBC are formed on the same base BC such that A and D lie on the opposite sides of BC such that AB= AC and DB=DC .Also AD intersects BC at O.
To show AD is the Perpendicular bisector ot BC ie. AD⊥BC and AD bisects BC .
Proof in ΔABDandΔACD
AB=AC [given ]
AD=AD [common side ]
and BD=DC [given ]
∴ΔABD≅ΔACD [by SSS congruence rule ]
⇒∠BAD=∠CAD[by CPCT ]
in ΔAOBandΔAOC
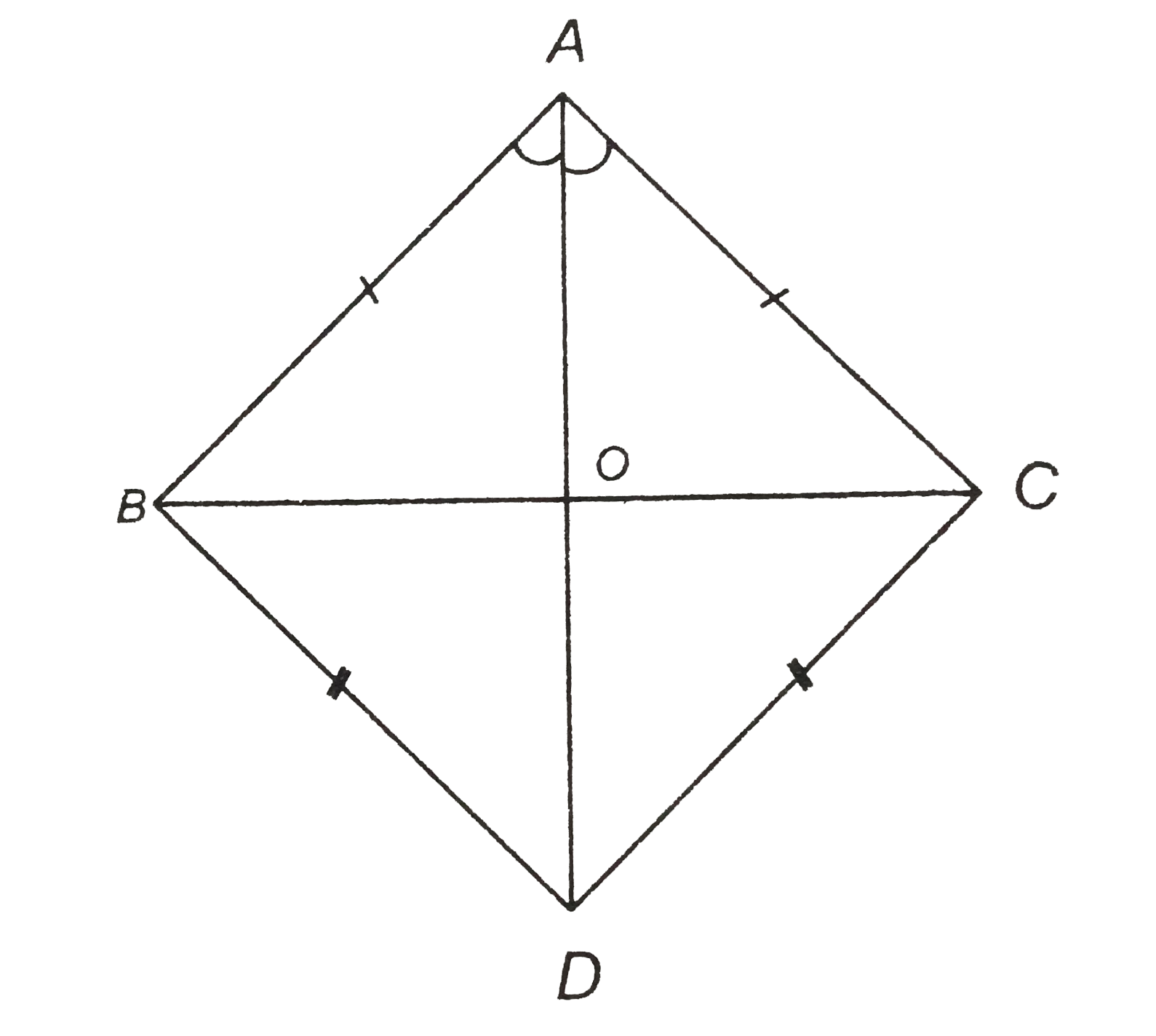
AB=AC [given]
AO =OA [common side ]
and ∠BAO=∠CAO [proved above ]
∴∠AOB≅ΔAOC [by CPCT]
but ∠AOB+∠AOC=180∘ [linear pair axiom ]
⇒∠AOB+∠AOB=180∘ [from Eq.(i) ] ltbr gt ⇒2∠AOB=180∘
⇒∠AOB=180∘2=90∘
Hence ,AD⊥BCand AD bisects BC i.e AD is the perpendicualr bisector
Topper's Solved these Questions
Similar Questions
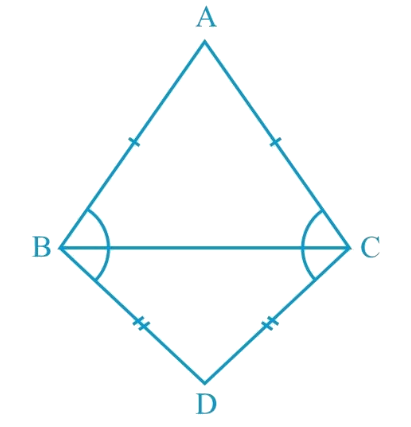
In Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn Figure, ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that ∠ABD= ∠ACD
View SolutionABC and DBC are both isosceles triangles on a common base BC such that A and D lie on the same side of BC. Are triangles ADB and ADC congruent? Which condition do you use? If ∠BAC=400 and ∠BDC =1000; then find ∠ADB
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
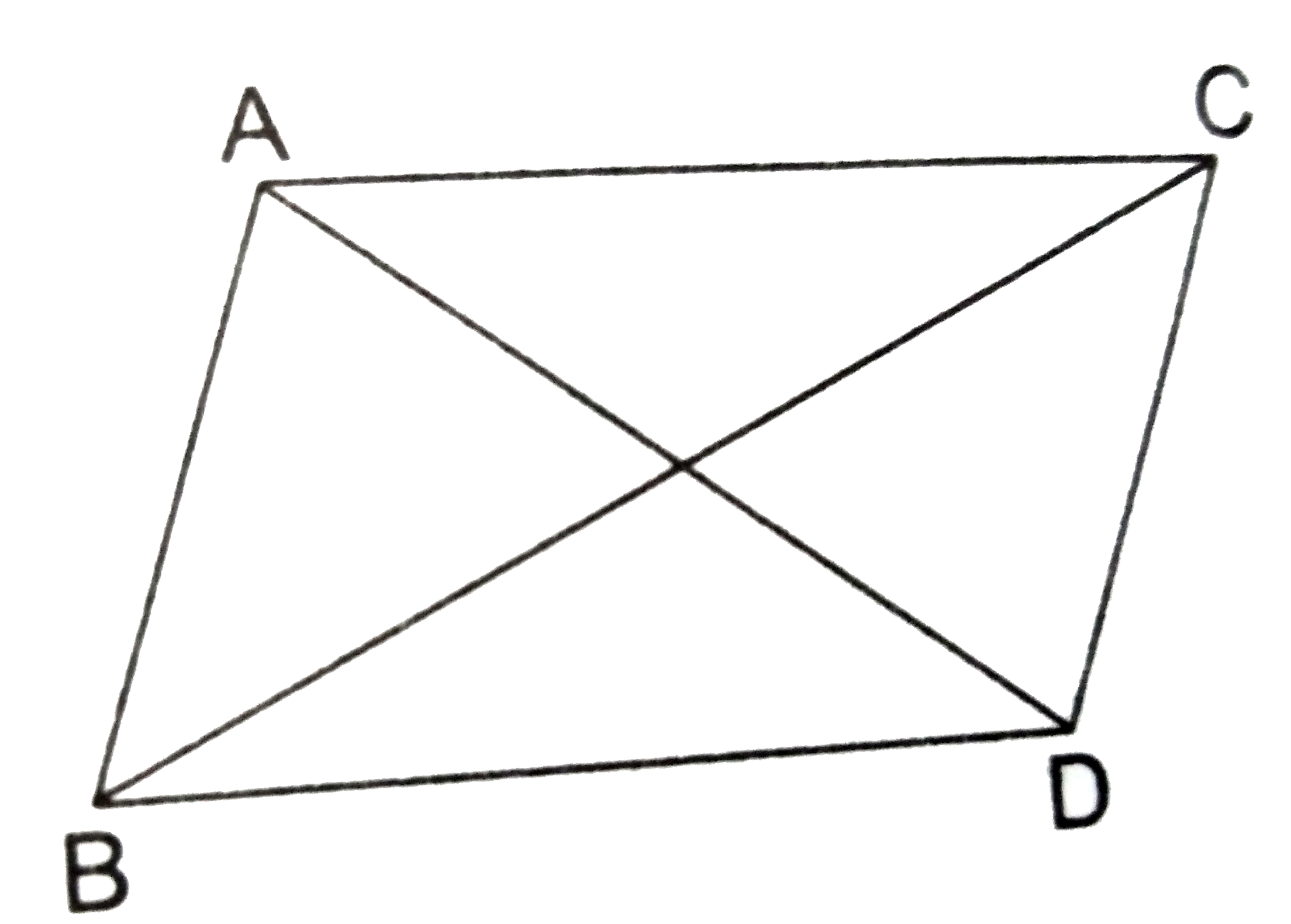
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionD is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View Solution
