ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
(a) area (ΔBCP) = area (ΔDPQ)
(b) area (ΔBCP)> area (ΔDPQ)
(c) area (ΔBCP)< area (ΔDPQ)
(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD)
The correct Answer is:A
To solve the problem, we need to analyze the given information about the parallelogram ABCD and the extension of line BC to point Q such that BC = CQ. We will compare the areas of triangles ABC and DCQ.
1. Identify the Given Information:
- ABCD is a parallelogram.
- BC is extended to point Q such that BC = CQ.
2. Understand the Properties of Parallelograms:
- In a parallelogram, opposite sides are equal, and opposite angles are equal.
- Additionally, consecutive angles are supplementary.
3. Analyze Triangles ABC and DCQ:
- We need to compare the areas of triangle ABC and triangle DCQ.
- Since BC = CQ, we can denote the length of BC as x. Therefore, CQ is also x.
4. Identify Corresponding Angles:
- Since ABCD is a parallelogram, we know:
- Angle ABC = Angle DCQ (corresponding angles).
- Angle A = Angle D (alternate interior angles).
5. Apply the Angle-Side-Angle (ASA) Congruence Criterion:
- We have:
- Angle ABC = Angle DCQ (from step 4).
- Angle A = Angle D (from step 4).
- Side BC = Side CQ (given).
- Therefore, by the ASA criterion, triangle ABC is congruent to triangle DCQ.
6. Conclude About the Areas:
- Since triangle ABC is congruent to triangle DCQ, their areas are equal.
- Thus, Area of triangle ABC = Area of triangle DCQ.
Final Answer:
The area of triangle ABC is equal to the area of triangle DCQ.
- ABCD is a parallelogram.
- BC is extended to point Q such that BC = CQ.
- In a parallelogram, opposite sides are equal, and opposite angles are equal.
- Additionally, consecutive angles are supplementary.
- We need to compare the areas of triangle ABC and triangle DCQ.
- Since BC = CQ, we can denote the length of BC as x. Therefore, CQ is also x.
- Since ABCD is a parallelogram, we know:
- Angle ABC = Angle DCQ (corresponding angles).
- Angle A = Angle D (alternate interior angles).
- We have:
- Angle ABC = Angle DCQ (from step 4).
- Angle A = Angle D (from step 4).
- Side BC = Side CQ (given).
- Therefore, by the ASA criterion, triangle ABC is congruent to triangle DCQ.
- Since triangle ABC is congruent to triangle DCQ, their areas are equal.
- Thus, Area of triangle ABC = Area of triangle DCQ.
The area of triangle ABC is equal to the area of triangle DCQ.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
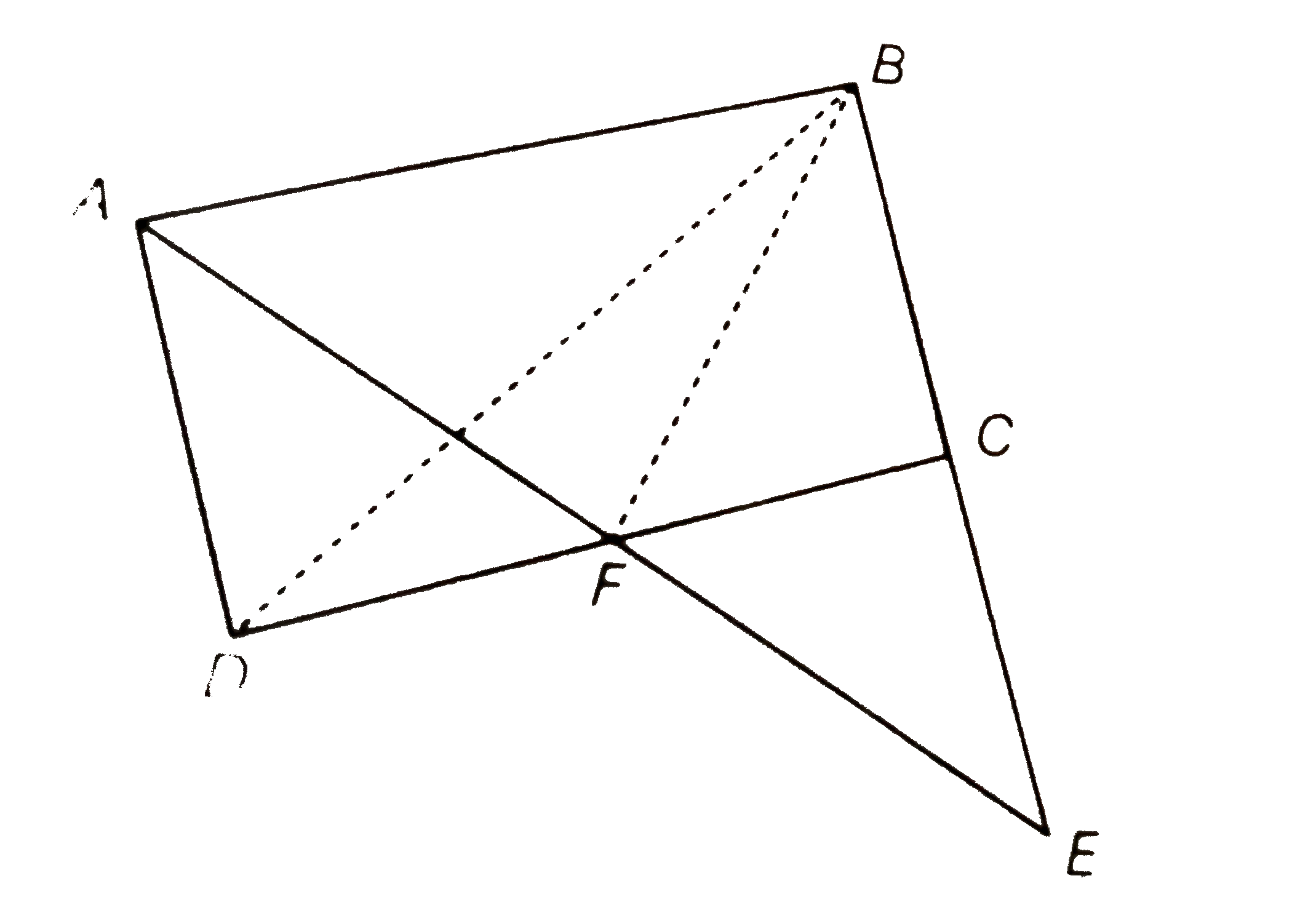
If ar(ΔDFB)=3cm2, then find the area of the parallelogram ABCD.View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
In the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
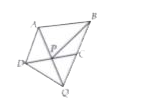 View Solution
View SolutionABCD is a parallelogram. AB is produced to E so that BE=AB . Prove that ED bisects BC.
View SolutionIn the adjoining figure, ABCD is a paralogram. The side AB is produced to P such that AB=BP and the side AD is produced to Q such that AD = DQ. Prove that CP = CQ.
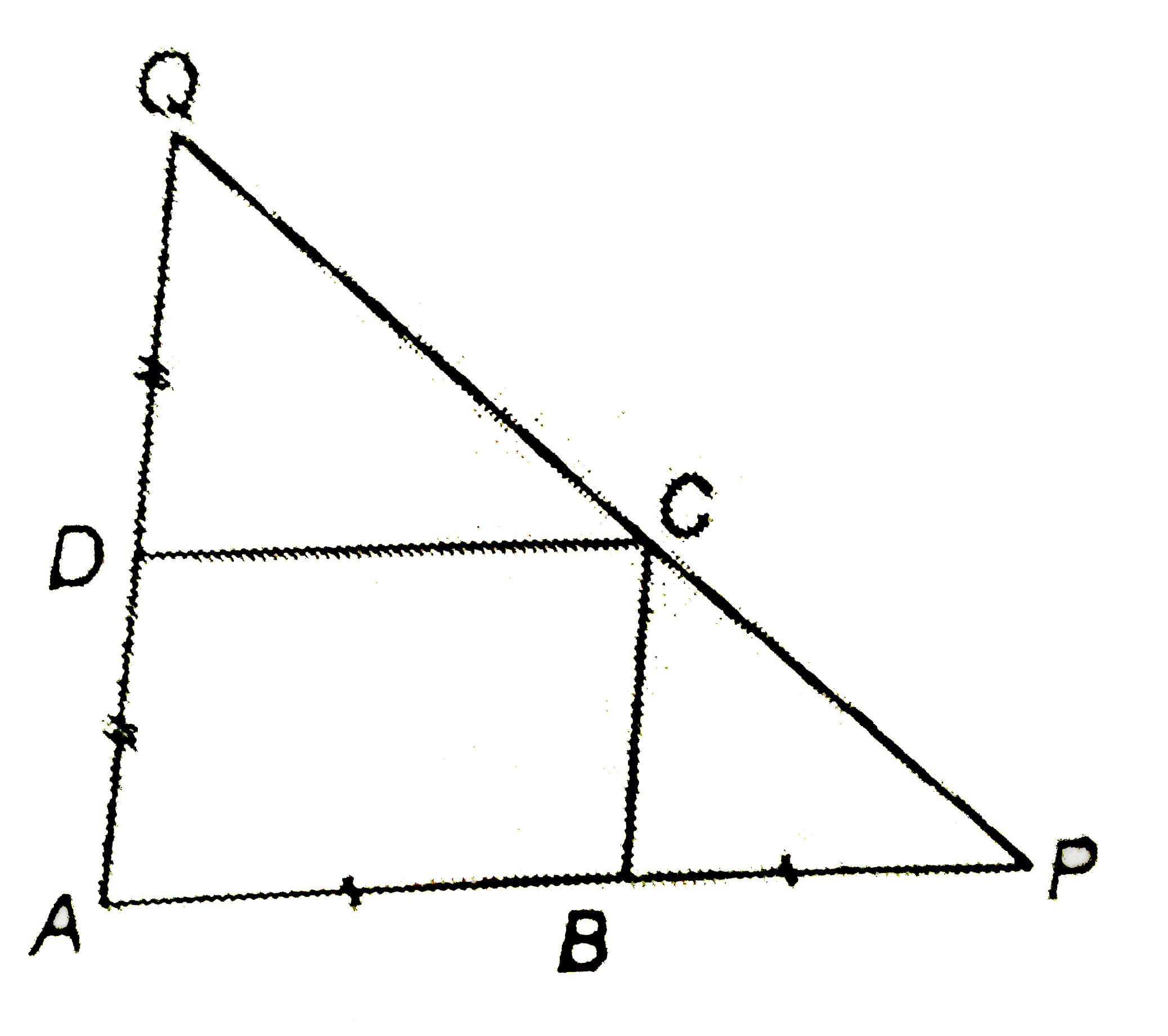 View Solution
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
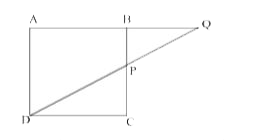 View Solution
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
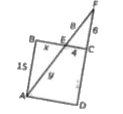 View Solution
View SolutionABCD is a parallelogram. Side AB is produced on both sides to E & F as in figure such that BE = BC & AF = AD. Show that EC & FD when produced meets at right angle.
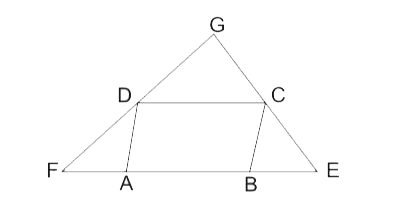 View Solution
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View Solution

