ABC is a given triangle. AD, BE and CF are altitudes of ΔABC.
Assertion (A) : (AB2+BC2+CA2)>(AD2+BE2+CF2)
Reason (R) : (AE2−AF2)+(BF2−BD2)+(CD2−CE2)=0
Both Assertion A and Reason R are correct and Reason R is a correct explanation of Assertion A.
Both Assertion A and Reason R are correct but Reason R is not the correct explanation of Assertion A.
Assertion A is correct, Reason R is wrong.
Assertion A is wrong, Reason R is correct.
The correct Answer is:B
To solve the assertion and reason question regarding triangle ABC and its altitudes AD, BE, and CF, we will analyze both statements step by step.
1. Understanding the Assertion:
The assertion states that AB2+BC2+CA2>AD2+BE2+CF2. This is a known property in geometry where the sum of the squares of the sides of a triangle is always greater than the sum of the squares of the altitudes.
Hint: Recall the property of triangles that relates the sides and altitudes.
2. Analyzing the Reason:
The reason given is AE2−AF2+BF2−BD2+CD2−CE2=0. This equation suggests a relationship between segments created by the altitudes and points on the sides of the triangle.
Hint: Check if the segments can be rearranged or if they hold any geometric significance.
3. Rearranging the Reason:
If we rearrange the equation, we can express it as:
AE2+BF2+CD2=AF2+BD2+CE2
This implies a balance between these segments. However, this does not hold true for all triangles, as the segments are not necessarily equal.
Hint: Consider whether the segments can be equal in all cases or if there are specific conditions required.
4. Conclusion on the Reason:
Since the equality in the reason does not hold for all triangles, we conclude that the reason is incorrect.
Hint: Think about specific examples of triangles to test the validity of the reason.
5. Final Evaluation:
The assertion is correct while the reason is incorrect. Therefore, we conclude that:
- Assertion (A) is true.
- Reason (R) is false.
Final Answer:
- Assertion (A) is correct.
- Reason (R) is incorrect.
The assertion states that AB2+BC2+CA2>AD2+BE2+CF2. This is a known property in geometry where the sum of the squares of the sides of a triangle is always greater than the sum of the squares of the altitudes.
The reason given is AE2−AF2+BF2−BD2+CD2−CE2=0. This equation suggests a relationship between segments created by the altitudes and points on the sides of the triangle.
If we rearrange the equation, we can express it as:
AE2+BF2+CD2=AF2+BD2+CE2
This implies a balance between these segments. However, this does not hold true for all triangles, as the segments are not necessarily equal.
Since the equality in the reason does not hold for all triangles, we conclude that the reason is incorrect.
The assertion is correct while the reason is incorrect. Therefore, we conclude that:
- Assertion (A) is true.
- Reason (R) is false.
- Assertion (A) is correct.
- Reason (R) is incorrect.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B28videos
ALGEBRAIC IDENTITIES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
Similar Questions
Knowledge Check
- Question 1 - Select One
If AD, BE and CF are the medians of a ABC ,then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
A4:3B3:2C3:4D2:3 - Question 2 - Select One
In the given triangle ABC,CD,BFandAE are the altitudes. If the ratio of CD:AE:BF=2:3:4, then the ratio of AB:BC:CA is :
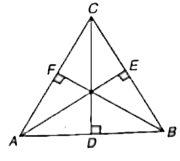A4:3:2B2:3:4C4:9:16D6:4:3
In ΔABC if AD is the median the show that AB2+AC2=2(AD2+BD2)
View SolutionAD,BE and CF are the medians of a ΔABC. Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionLet ABC and A'B'C' be two triangles in which AB>A'B',BC>B'C'andCA>C'A'. Let D, E and F be the midpoints of the sides BC, CA and AB respectively. Let D', E' and F' be the midpoints of the sides B'C', C'A' and A'B' respectively. Consider the following statements :
Statement I:
AD>A'D',BE>B'E'andCF>C'F'
are always true.
Statement II :
AB2+BC2+CA2AD2+BE2+CF2=A'B'2+B'C'2+C'A'2A'D'2+B'E'2+C'F'2
Which one of the following is correct in respect of the above statements?View SolutionIf ABC is an isosceles triangle and D is a point on BC such that AD⊥BC , then AB2−AD2=BD.DC (b) AB2−AD2=BD2−DC2 (c) AB2+AD2=BD.DC (d) AB2+AD2=BD2−DC2
View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2View Solution