PQ is a lines segment and R is its midpoint. Semicircles are drawn at the same side of PQ taking PR,RQandPQ as diameters. A circle of radius r and centre O is drawn touching all the three semi circles.
Prove that r=16PQ
Step by step video & image solution for PQ is a lines segment and R is its midpoint. Semicircles are drawn at the same side of PQ taking PR, RQ and PQ as diameters. A circle of radius r and centre O is drawn touching all the three semi circles. Prove that r = (1)/(6) PQ by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8A
71 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
Similar Questions
In the figure semicircles are drawn with PQ, PB and BQ as diameter. PB=BQ=21cm. A circle with centre O is drawn to touch all the three semicircles. Find its radius and also find the shaded region.

View Solution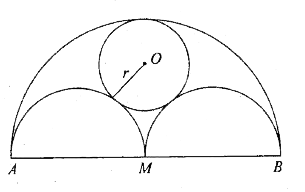
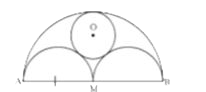
AB is a line segment of length 2a with M as mid-point. Semicircles are drawn on one side with AM, MB and AB as diameter as shown in the above figure. A circle .with centre O and radius r is drawn such that this circle touches all the three semicircles. The value of r is
View Solution
Knowledge Check
PQ is a lines segment of 12 cm whose midpoint is R. Taking PR, RQ and PQ as diameters semicircles are drawn at the same side of PQ. The area of the circle that touches all the three circles is
A2πsq. cmB4π sq. cmC6π sq. cmD94 sq. cmLet PQandRS be tangent at the extremities of the diameter PR of a circle of radius r. If PSandRQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQxRS .
A√PQ.RSBPQ+RS2C2PQ.RSPQ+RSD√PQ2+RS22
PQ is a line segment 12cm long and R is a point in its interior such PR=8cm,then
View SolutionIn the given figure, AB is a line of length 2a and mid Point M. Taking AM, MB and AB as diameters semi circles are drawn on the same sides of the line. Taking centre O and radius 'r' a circle is drawn such that it touches all the three circles. Then find the value of r.
View SolutionPS is the diameter of a circle of radius 6 cm. The points Q and R cts the diameter Ps. Semi circles are drawn on PQ and Qs as diameters. Find the area of the shaded region.
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if ∠QPR=90∘, then length of PQ is
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals
View Solution
