PQR is an equilateral triangle. O is the point of intersection of altitudes PL,QM and RN. If OP=8cm, then what is the perimeter of the triangle PQR ?
8√3cm
12√3cm
16√3cm
24√3cm
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Understand the Properties of the Equilateral Triangle
Given that triangle PQR is equilateral, all sides are equal. Let's denote the length of each side as y. Therefore, we have:
- PQ=QR=PR=y
Hint: Remember that in an equilateral triangle, all sides and angles are equal.
Step 2: Identify the Point of Intersection of Altitudes
The point O is the orthocenter of the triangle, which is also the centroid in an equilateral triangle. The centroid divides each median in the ratio of 2:1.
Hint: The orthocenter and centroid coincide in an equilateral triangle.
Step 3: Define the Lengths of the Medians
Let PL be the median from point P to side QR. Since O divides PL in the ratio of 2:1, we can express the lengths:
- Let OP=2x and OL=x (where L is the midpoint of QR).
Since OP=8cm, we have:
2x=8⟹x=4cm
Hint: Use the given length of OP to find x.
Step 4: Calculate the Length of the Median
The total length of median PL is:
PL=OP+OL=2x+x=3x=3(4)=12cm
Hint: Remember that the median length can be expressed in terms of the sides of the triangle.
Step 5: Use the Median Length Formula
The length of the median m in terms of the side y of an equilateral triangle is given by:
m=√32y
Setting this equal to the calculated median length:
√32y=12
Hint: Familiarize yourself with the formula for the median in an equilateral triangle.
Step 6: Solve for the Side Length y
To find y:
y=12⋅2√3=24√3=8√3cm
Hint: Rationalize the denominator if necessary.
Step 7: Calculate the Perimeter of Triangle PQR
The perimeter P of triangle PQR is given by:
P=3y=3(8√3)=24√3cm
Hint: The perimeter of an equilateral triangle is three times the length of one side.
Final Answer
The perimeter of triangle PQR is 24√3cm.
---
Given that triangle PQR is equilateral, all sides are equal. Let's denote the length of each side as y. Therefore, we have:
- PQ=QR=PR=y
The point O is the orthocenter of the triangle, which is also the centroid in an equilateral triangle. The centroid divides each median in the ratio of 2:1.
Let PL be the median from point P to side QR. Since O divides PL in the ratio of 2:1, we can express the lengths:
- Let OP=2x and OL=x (where L is the midpoint of QR).
2x=8⟹x=4cm
The total length of median PL is:
PL=OP+OL=2x+x=3x=3(4)=12cm
The length of the median m in terms of the side y of an equilateral triangle is given by:
m=√32y
Setting this equal to the calculated median length:
√32y=12
To find y:
y=12⋅2√3=24√3=8√3cm
The perimeter P of triangle PQR is given by:
P=3y=3(8√3)=24√3cm
The perimeter of triangle PQR is 24√3cm.
Similar Questions
Knowledge Check
ΔABCis a equilateral triangle. O is the point of intcrscction of al titudes AL,BMandCN. If OA=16cm, what is the semi-perimeter (in cm) of the triangle ABC?
A8√3B12√3C16√3D24√3ΔABCis a equilateral triangle. O is the point of intcrscction of al titudes AL,BMandCN. If OA=16cm, what is the semi-perimeter (in cm) of the triangle ABC?
A8√3B12√3C16√3D24√3The midpoints of the sides of an equilateral triangle PQR are X, Y and Z. If the perimeter of triangle PQR is 24 cm. then what is the perimeter of triangle XYZ?
A96 cmB36 cmC12 cmD48 cm

In the figure above, PQRS is a parallelogram and G is the centroid of the triangle PQR . A is the point of intersection of the diagonals PR and SQ. If AG=3 cm, then find the length of SQ.
View Solution
In the figure above, PQRS is a parallelogram and G is the centroid of the triangle PQR . A is the point of intersection of the diagonals PR and SQ. If AG=3 cm, then find the length of SQ.
View SolutionABC is an equilateral triangle PQRS is a square inscribed in it there fore
View SolutionPQR is an equilateral triangle. MN is drawn parallel to QR such that M is on PQ and N is on PR. If PN = 6 cm, then the length of MN is
View SolutionAn equilateral triangle circumscribes all the three circles each of radius 1 cm . What is the perimeter of the equilateral triangle ?
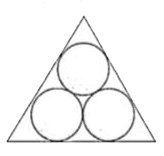
View Solution