If you are provided a set of resistances 2Ω,4Ω,6Ω and 8Ω. Connect these resistances so as to obtain an equivalent resistance of 463Ω
4Ω and 6Ω are in parallel with 2Ω and 8Ω in series
2Ω and 6Ω are in parallel with 4Ω and 8Ω in series
2Ω and 4Ω are in parallel with 6Ω and 8Ω in series
6Ω and 8Ω are in parallel with 2Ω and 4Ω in series
To solve the problem of obtaining an equivalent resistance of 463Ω using the resistances 2Ω,4Ω,6Ω, and 8Ω, we can explore different combinations of these resistances.
1. Understanding the Problem: We need to connect the given resistances in such a way that the total or equivalent resistance equals 463Ω.
2. Choosing Combinations: We can connect resistors in series or parallel. The formula for resistors in series is:
Rseries=R1+R2+…
The formula for resistors in parallel is:
1Rparallel=1R1+1R2+…
3. Testing Combinations: We will test different combinations of the resistors.
- Combination 1: Connect 4Ω and 6Ω in parallel, and then connect the result in series with 2Ω and 8Ω.
- Calculating Parallel Resistance:
1Rp=14+16
Finding a common denominator (12):
1Rp=312+212=512
Therefore,
Rp=125Ω
- Calculating Total Resistance:
Now, connect Rp in series with 2Ω and 8Ω:
Rtotal=Rp+2+8=125+2+8
Converting 2 and 8 to fractions with a denominator of 5:
2=105,8=405
Thus,
Rtotal=125+105+405=625Ω
This value is not equal to 463Ω.
4. Trying Another Combination:
- Combination 2: Connect 2Ω and 4Ω in parallel, and then connect this in series with 6Ω and 8Ω.
- Calculating Parallel Resistance:
1Rp=12+14
Finding a common denominator (4):
1Rp=24+14=34
Therefore,
Rp=43Ω
- Calculating Total Resistance:
Now, connect Rp in series with 6Ω and 8Ω:
Rtotal=Rp+6+8=43+6+8
Converting 6 and 8 to fractions with a denominator of 3:
6=183,8=243
Thus,
Rtotal=43+183+243=463Ω
This matches the required equivalent resistance.
Final Answer:
The equivalent resistance of 463Ω can be obtained by connecting 2Ω and 4Ω in parallel, and then connecting this combination in series with 6Ω and 8Ω.
Rseries=R1+R2+…
The formula for resistors in parallel is:
1Rparallel=1R1+1R2+…
1Rp=14+16
Finding a common denominator (12):
1Rp=312+212=512
Therefore,
Rp=125Ω
Now, connect Rp in series with 2Ω and 8Ω:
Rtotal=Rp+2+8=125+2+8
Converting 2 and 8 to fractions with a denominator of 5:
2=105,8=405
Thus,
Rtotal=125+105+405=625Ω
This value is not equal to 463Ω.
- Combination 2: Connect 2Ω and 4Ω in parallel, and then connect this in series with 6Ω and 8Ω.
1Rp=12+14
Finding a common denominator (4):
1Rp=24+14=34
Therefore,
Rp=43Ω
Now, connect Rp in series with 6Ω and 8Ω:
Rtotal=Rp+6+8=43+6+8
Converting 6 and 8 to fractions with a denominator of 3:
6=183,8=243
Thus,
Rtotal=43+183+243=463Ω
This matches the required equivalent resistance.
The equivalent resistance of 463Ω can be obtained by connecting 2Ω and 4Ω in parallel, and then connecting this combination in series with 6Ω and 8Ω.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
Knowledge Check
If you are provided three resistances 2Ω,3Ω and 6Ω. How will you connect then so as to obtain the equivalent resistance of 4Ω ?
A B
B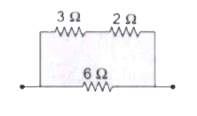 C
C Dnone of these
Dnone of theseIf you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
A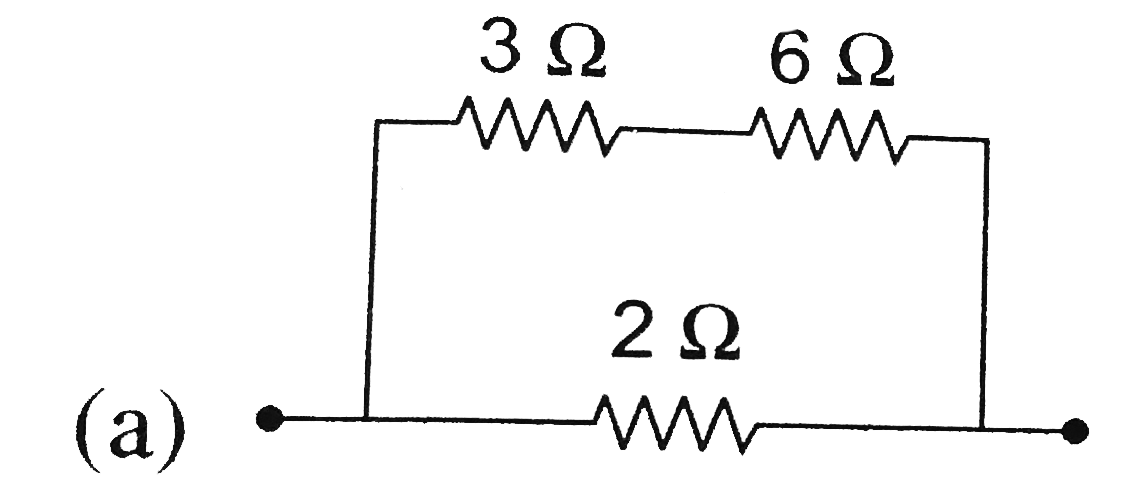 B
B C
C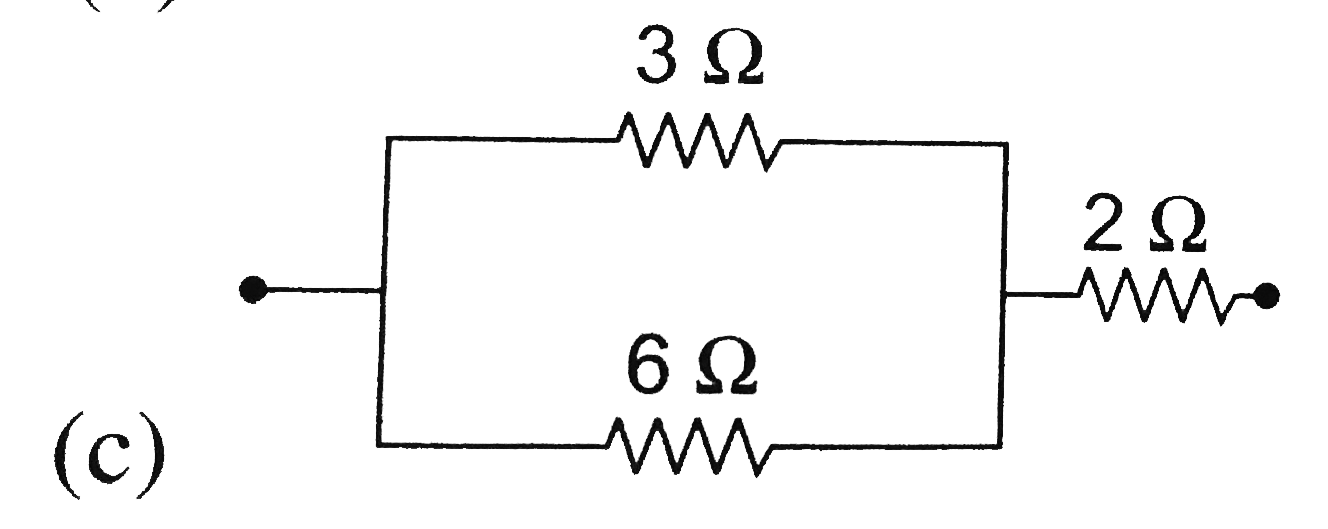 Dnone
DnoneThe resistors of resistances 2Ω,4Ω and 8Ω are connected in parallel, then the equivalent resistance of the combination will be
A87ΩB78ΩC74ΩD49Ω
How will you join the resistors of resistances 3Ω,6Ω and 8Ω to get an equivalent resistance of 10Ω?
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionYou have two metallic wires of resistances 6Ωand3Ω. How will you connect these wires to get the effective resistance of 2Ω?
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionIf three resistors of resistance 2Ω,4Ω and 5Ω are connected in parallel then the total resistance of the combination will be
View Solution
