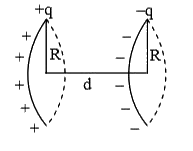
Two thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -

$\frac{Q}{2 π e s π_{0}} [\frac{1}{a} - \frac{1}{\sqrt{s^{2} + a^{2}}}]$

$\frac{Q}{2 π e s π_{0}} [\frac{1}{a} + \frac{1}{\sqrt{s^{2} + a^{2}}}]$

$\frac{Q}{4 π e s π_{0}} [\frac{1}{a} - \frac{1}{\sqrt{s^{2} + a^{2}}}]$

$\frac{Q}{4 π e s π_{0}} [\frac{1}{a} + \frac{1}{\sqrt{s^{2} + a^{2}}}]$

Video Solution

Answer

Step by step video & image solution for Two thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are $+ q$ and $- q$ . The potential difference between the centres of the two rings is
A(a) $\frac{q}{2 π \in_{0}} [\frac{1}{R} - \frac{1}{\sqrt{R^{2} - d^{2}}}]$
B(b) $\frac{q R}{4 π \in_{0} d^{2}}$
C(c) $\frac{q}{4 π \in_{0}} [\frac{1}{R} - \frac{1}{\sqrt{R^{2} + d^{2}}}]$
D(d) zero
Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are $+ Q$ and $- Q$ . The potential difference between the centre so the two rings is
Azero
B $\frac{Q}{4 π ε_{0}} [\frac{1}{R} - \frac{1}{\sqrt{R^{2} + d^{2}}}]$
C $\frac{Q}{4} π ε_{0} d^{2})$
D $\frac{Q}{2 π ε_{0}} [\frac{1}{R} - \frac{1}{\sqrt{R^{2} + d^{2}}}]$
A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge $Q (R > r 0$ . The potential difference between the two is
AProportional to Q
BProportional to q
CDependent on both Q and q
DIndependent of both Q and q

JEE MAINS PREVIOUS YEAR-JEE MAINS 2021-Physics (Section A )

Home
Ask Doubt
Profile

Two thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is

Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is

A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q(R>r0. The potential difference between the two is

JEE MAINS PREVIOUS YEAR-JEE MAINS 2021-Physics (Section A )

Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are $+ q$ and $- q$ . The potential difference between the centres of the two rings is

Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are $+ Q$ and $- Q$ . The potential difference between the centre so the two rings is

A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge $Q (R > r 0$ . The potential difference between the two is