Consider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for d>>x, the magnetic field at P varies as (1/d^2) whereas for d << x, it varies as 1/d.Solution in Tamil
Since O is the mid point of MN=l.
So , B=μoi4π. 2l√l2+4d2.
If d>>x,thusB=μoi4πd. 2l2d.
i.e. B∝1d .

Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMAChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Objective 2
Explore 7 Videos
- MAGNETIC FIELDBook:HC VERMAChapter:MAGNETIC FIELDExercise:Exercises
Explore 60 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMAChapter:MAGNETIC PROPERTIES OF MATTERExercise:Exercise
Explore 9 Videos
Similar Questions
The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionA long, straight wire carries a current i. Let B_1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section. Let B_2 be the magnetic field at this point due to this section only. Find the value of d/l so that B_2 differs from B_1 by 1 %.
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)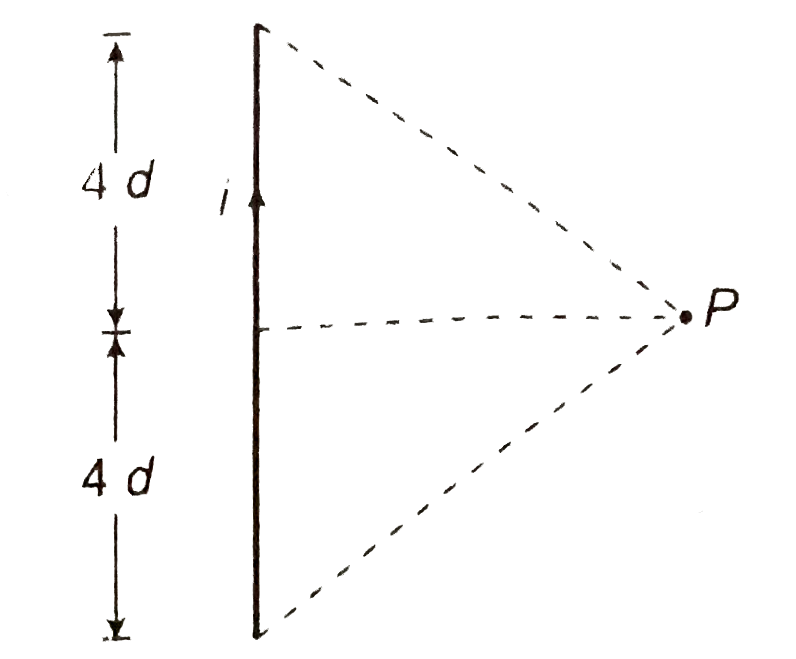
(b)
P is the centre of square.
(c)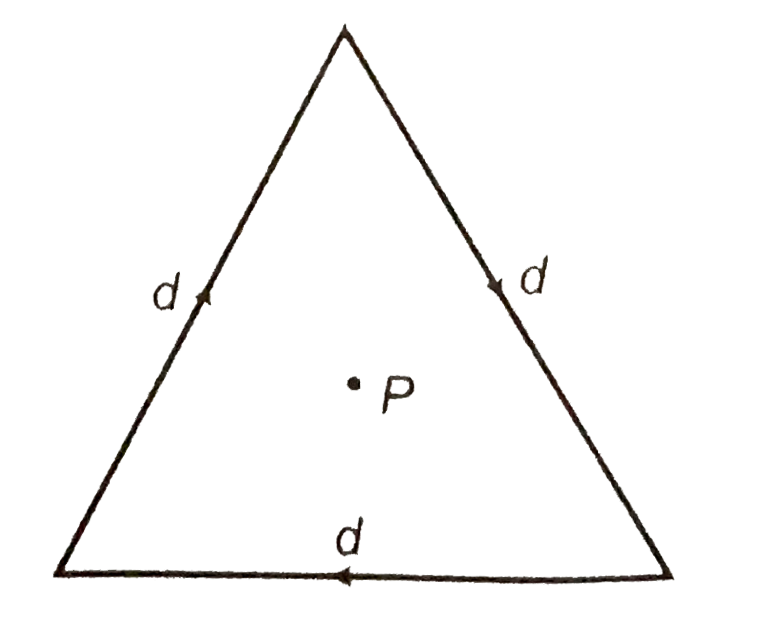
P is the centre of equilateral triangle.
(d)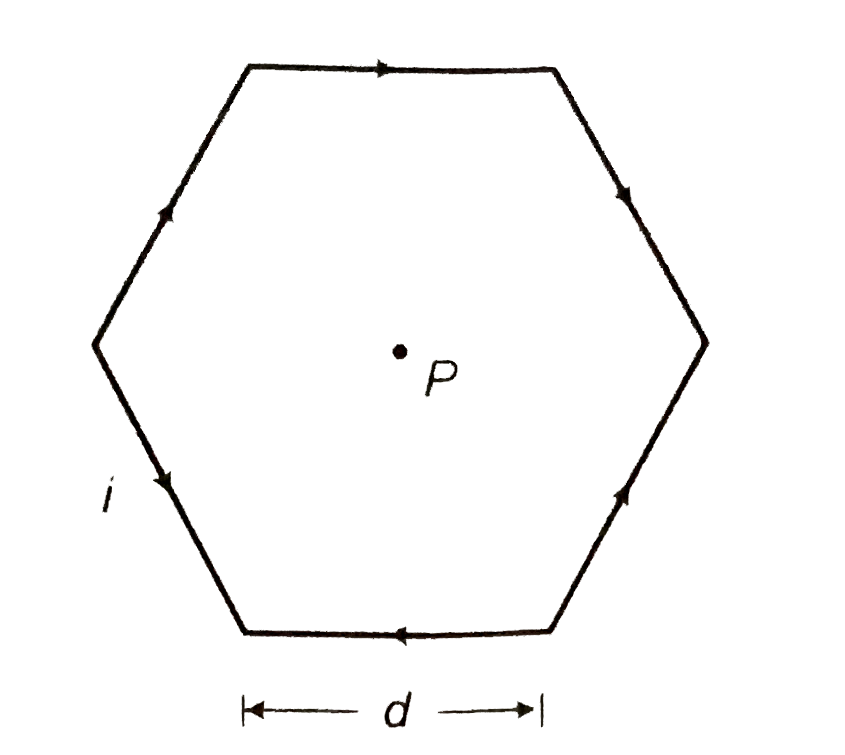
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)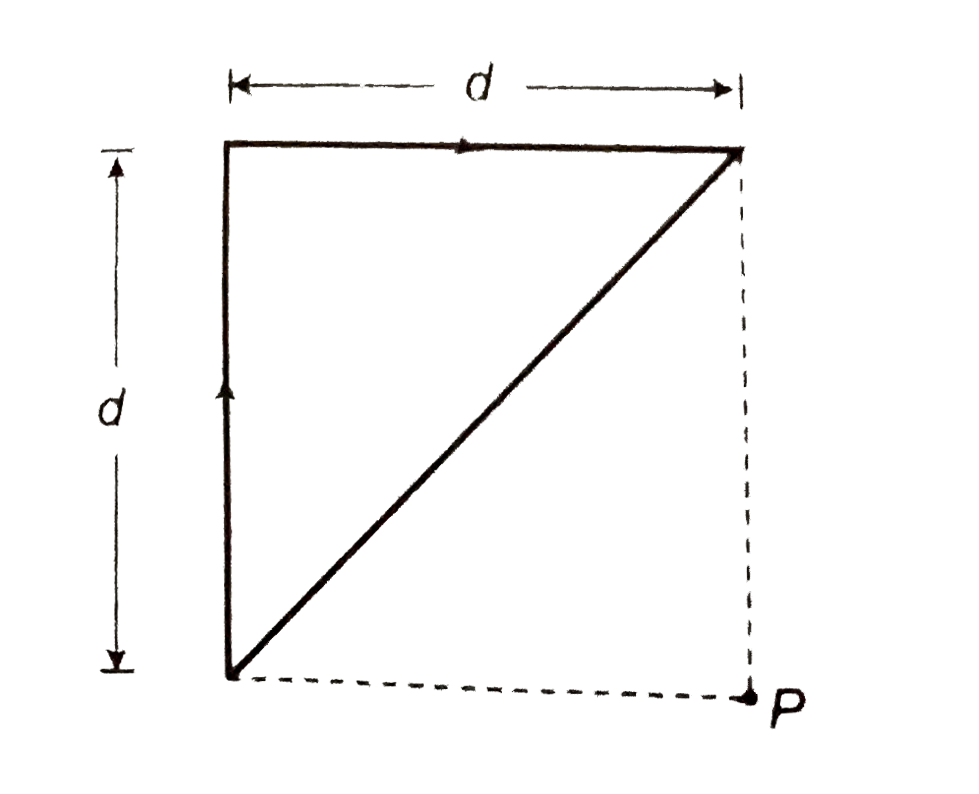
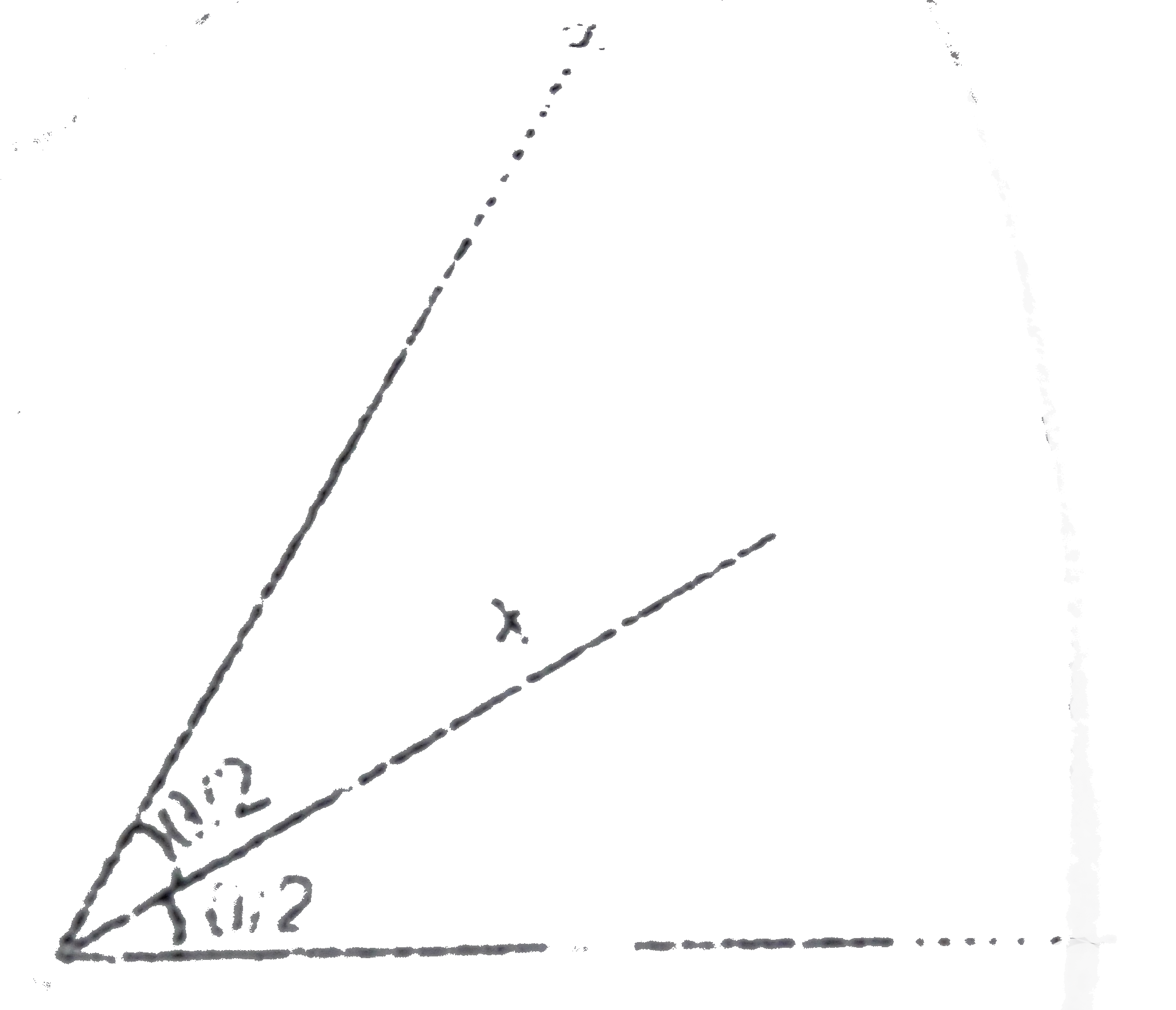
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View SolutionA long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
View SolutionThe magnetic flux density at a point distant d from a long straight current carrying conductor is B, then its value at distance d2 will be-
View SolutionAbB is a section of a straight wire carrying a current I . P is a point at a distance d from AB . The magnetic field at P due to AB has magnitude
View SolutionA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)

View SolutionThe magnetic field due to a current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r(r>>L)
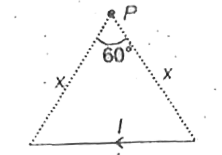
View SolutionA straight wire of finite length carrying current I subtends an angle of 60∘ at point P as shown. The magnetic field at P is
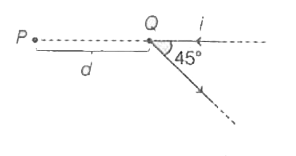
View SolutionA long straight wire carrying electric current i is bent at its mid-point to form an angle of 45∘ as shown in the figure. Magnetic field at a point P at a distance d from the point Q of bending is
View Solutionअनंत लम्बाई के धारावाही चालक तार के अभिलंबवत d दुरी पर किसी बिंदु p पर चुंबकीय क्षेत्र का मान कितना होगा यदि तार में प्रवाहित धारा I हो ?
View SolutionAB is a section of a straight wire carrying a current I.P is a point at a distance d from AB . the magnetic field at P due to AB has magnitude :
View SolutionTwo long straight parallel wires A and B separated by a distance d, carry equal current I flowing in same direction as shown in the figure.
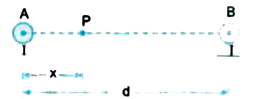
(a) Find the magnetic field at a point P situated between them at a distance x from one wire.
(b) Show graphically the variation of the magnetic field with distance x for 0<x<d.
View SolutionA long, straight wire carries a current i. Let B_1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section. Let B_2 be the magnetic field at this point due to this section only. Find the value of d/l so that B_2 differs from B_1 by 1 %.
View Solution