A conducting disc of radius r rotaes with a small but constant angular velocity about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.Solution in Tamil
Velocity at a dostance from the centre= (r omega)/2E=Blv=Bxxrxx(r omega)/2=(1/2)Br^2 omega.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise9videos
ELECTROMAGNETIC WAVES
Similar Questions
A bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
02:57View SolutionFind the dimensional formula of ε0 .
07:11View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
08:03View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
05:37View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
09:18View SolutionA metal disc of radius R = 25 cm rotates with a constant angular velocity omega = 130 rad s^(-1) about its axis. Find the potential difference between the center and rim of the disc if (a) the external magnetic field is absent, (b) the external uniform megnetic field B = 5.0 mT directed perpendicular to the disc.
03:20View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
01:44View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density sigma rotates about its axis with an angular velocity omega . Find : (a) the magnetic induction at the centre of the disc, (b) the magnetic moment of the disc. ( c) the ratio of magnetic moment and angular momentum of disc.
01:53View Solutiona conducting disc of radius R roatates about its axis when an angular velocity omega .Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
06:38View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity omega in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
03:08View SolutionA metal disc of radius R rotates with an angular velcoity ω about an axis perpendicular to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
04:01View SolutionA non-conducting disc having unifrom positive charge Q , is rotating about its axis with unifrom angular velocity omega .The magnetic field at the centre of the disc is.
05:56View SolutionFigure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed ω=40rad/s,B=0.10T and R=1Ω. The current through the resistor is
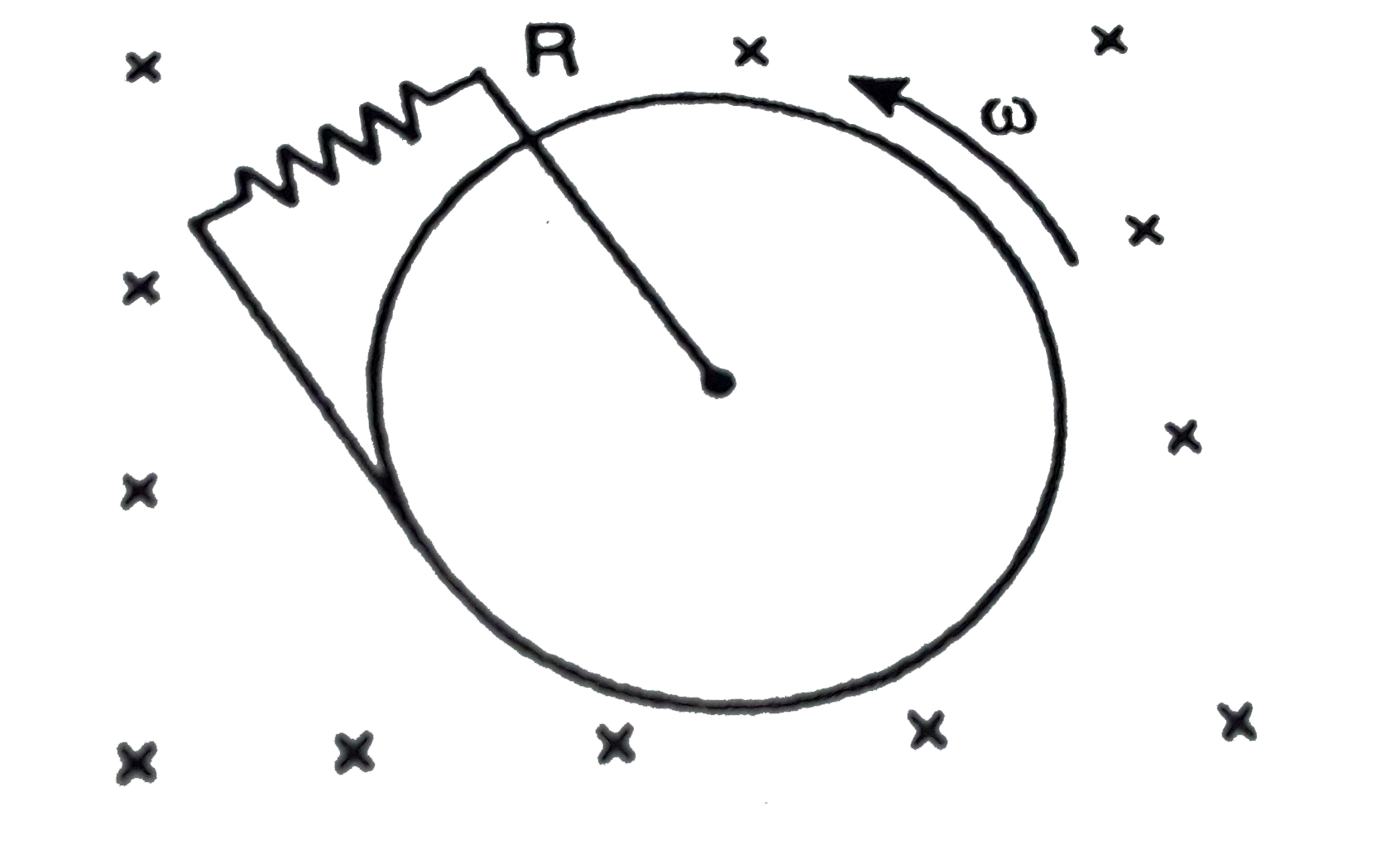 05:28View Solution
05:28View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
06:25View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
06:45View SolutionA circular metalic disc of radius a is rotating with a uniform angular velocity (w) perpendicularly to the uniform magnetic field →B. The potential difference between the centre and the rim of the disc is—
02:36View Solution

