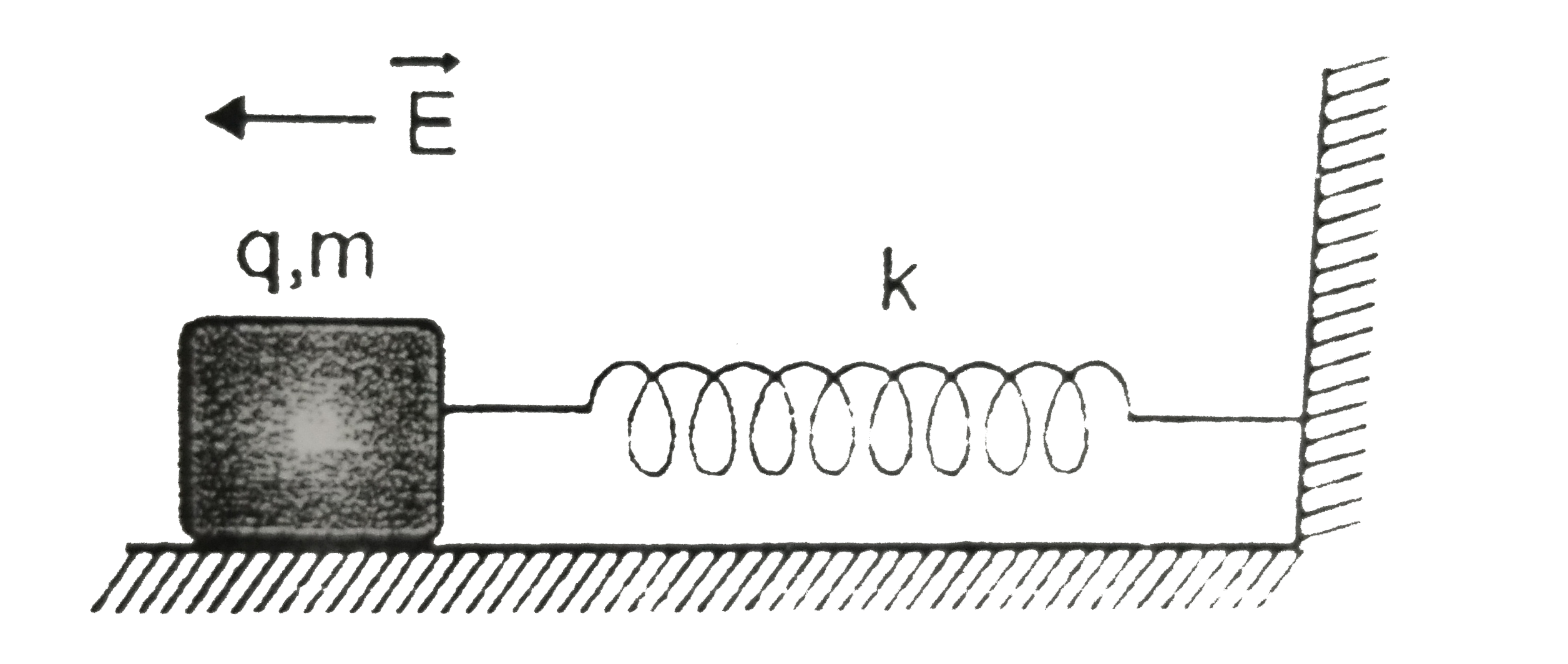
A particle of mass m and having a charge q is placed on a smooth horizontal table and is connected to walls through unstreched springs of constant k ( shown in figure ). A horizontal electric field E parallel to spring is switched on. The maximum speed of the particle is :
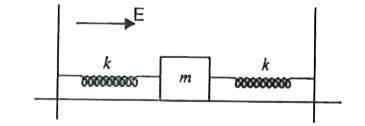
qE√2mk
qEmk
qEm
None of these
The correct Answer is:A
Two springs of same spring constant are in parallel
Then effective spring constant k. = 2k
At equilibrium 2kxmax=qE
ω=√2km
∴ 12mv2mx=12mA2ω2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL-III
23 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS
39 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS
39 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
8 Videos
Similar Questions
A block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.
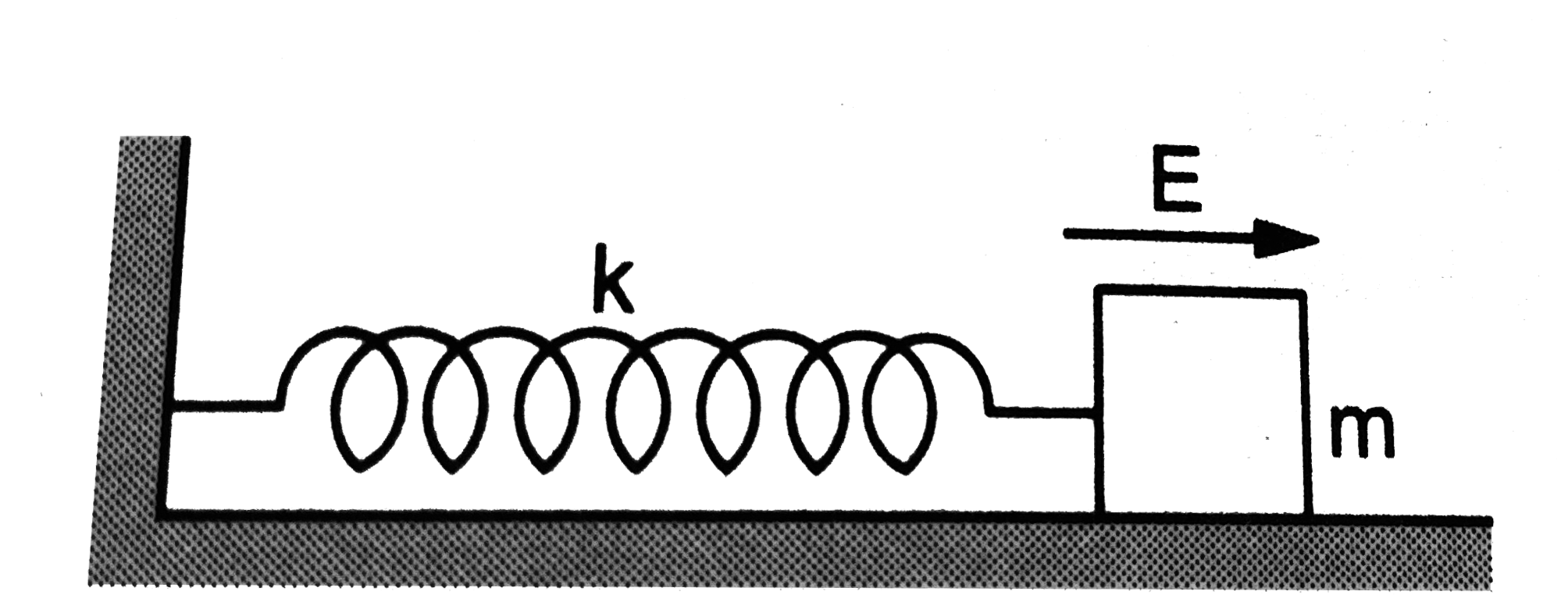
View SolutionA block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.

View Solution
Knowledge Check
A particular of mass m and having a charge q is placed on a smooth horizontal table and is connected to walls through unstressed springs of constant k (shown in figure). A horizontal electric field E parallel to spring is switched On. The maximum speed of the particle
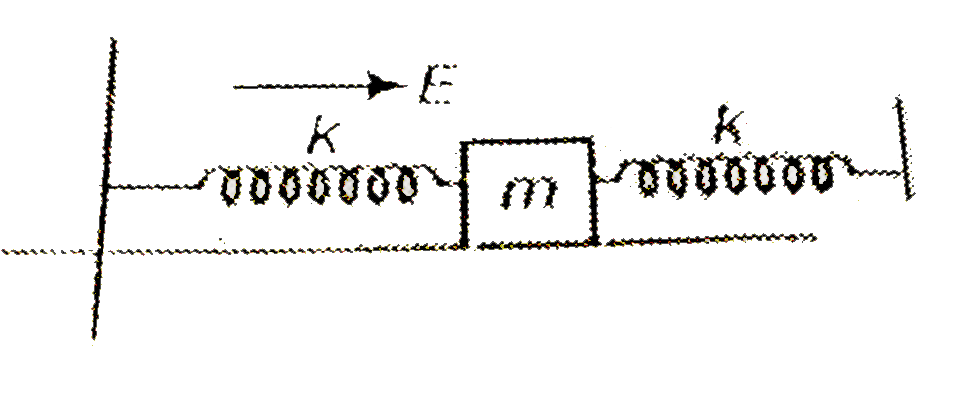 AqE√(2mk)BqEmkCqEmDnone of these
AqE√(2mk)BqEmkCqEmDnone of theseA block of mass m containing a net negative chage −q is placed on a froctionless horizontal tabe and is connected to a wall through an unstreached spring of spring constant k. If the horizontal electric field E parallel to spring is switched on , then the maximum compression of the spring is
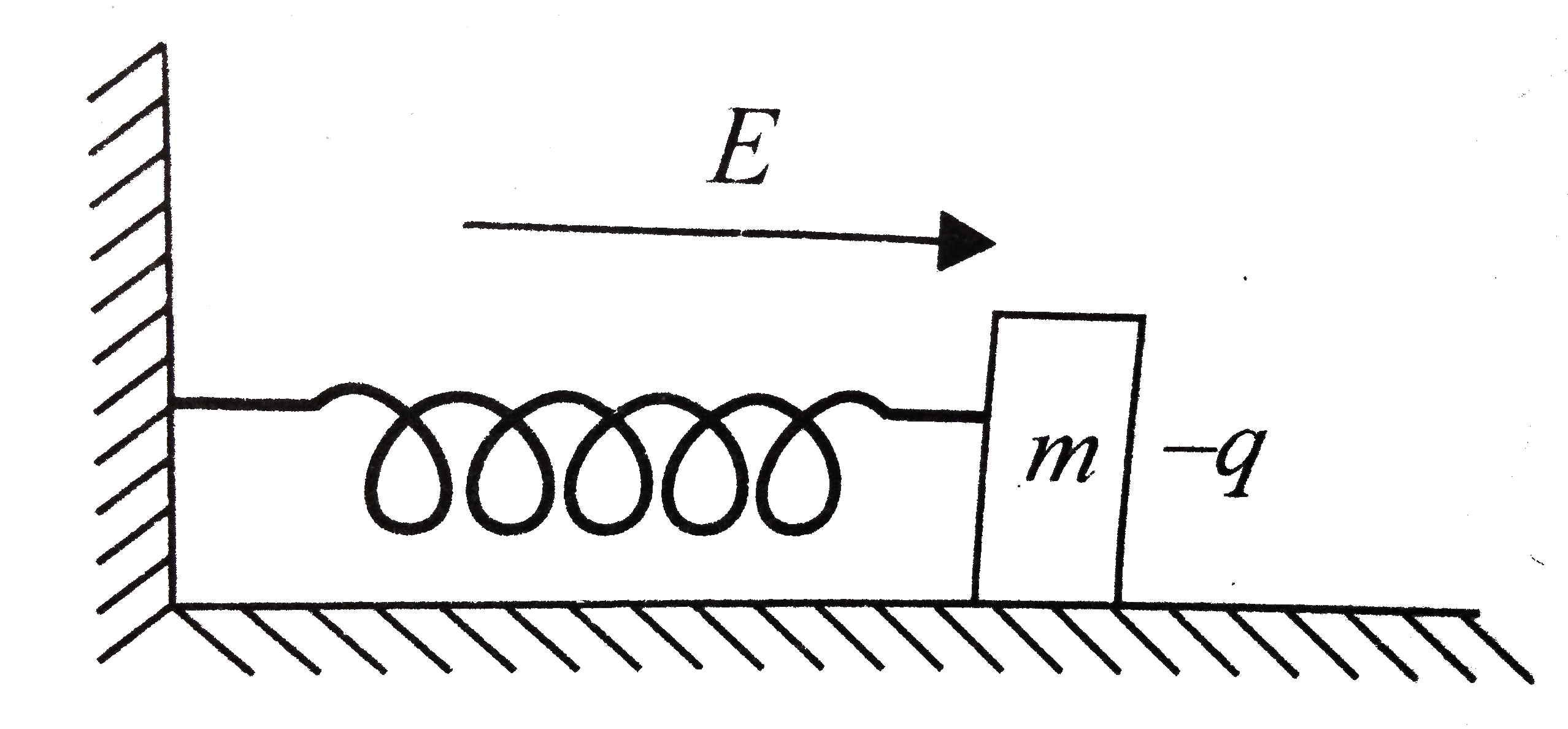 A√qE/kB2qE/kCqE/kDzero
A√qE/kB2qE/kCqE/kDzeroA spring mass system as shown in figure is suspended in a constant electric field E. A charge q is given to the mass.
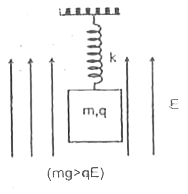 ATime period of oscillation of the system is 2π√mkBTime period of oscillation of the system is 2π√mg−qEkCThe elongation is the spring in equilibrium position will be mg−qEkDThe elongation is the spring in equilibrium position will be mgk
ATime period of oscillation of the system is 2π√mkBTime period of oscillation of the system is 2π√mg−qEkCThe elongation is the spring in equilibrium position will be mg−qEkDThe elongation is the spring in equilibrium position will be mgk
A block of mass m containing a net negative chage −q is placed on a froctionless horizontal tabe and is connected to a wall through an unstreached spring of spring constant k. If the horizontal electric field E parallel to spring is switched on , then the maximum compression of the spring is

View SolutionA small cork block of mass m=1kg having charge q=−1C placed on a rough horizontal surface and is connected to a vertical wall through an unstretched non conducting light spring of spring consant k=9N/m as shown in the figure. If a horizontal constant electric field E=10N/C is switched on then the maximum compression in the spring is xm. Find the value of x. (Take g=10m/s2,μ=0.1)
View SolutionA small cork block of mass m=1kg having charge q=−1C placed on a rough horizontal surface and is connected to a vertical wall through an unstretched non conducting light spring of spring consant k=9N/m as shown in the figure. If a horizontal constant electric field E=10N/C is switched on then the maximum compression in the spring is xm. Find the value of x. (Take g=10m/s2,μ=0.1)

View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View Solution
