Spherical symmetric charge system centred at origin electric potential ϕ=Q4π∈0R0r≤R0
=Q4π∈0r,rR0 :
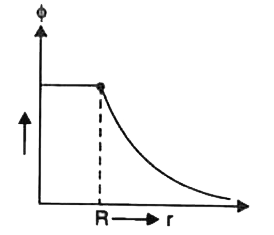
A spherical symmetry at r = 2R0 encloses a net charge Q
Electric field is discontinued at r=R0
Charge is only present at r=R0
Electrostatic energy is zero for r<R0
The correct Answer is:A, B, C
(a,b,c) For r>R0E=−dϕdr=Q4π∈0r2
∴Charge enclosed by concentric spherical surface of r
=2R0=∈0ϕE=∈0R4πr2
=∈0Q4π∈0r24πr2=Q For r<R0,E=−dVdr=0 and for r>R0
E=−dVdr=4π∈0r2 (Here V=ϕ)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL-III
23 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS
39 Videos
- ELECTROSTATICSBOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS
39 Videos
- ELECTRONS & PHOTONSBOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions
8 Videos
Similar Questions
A spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
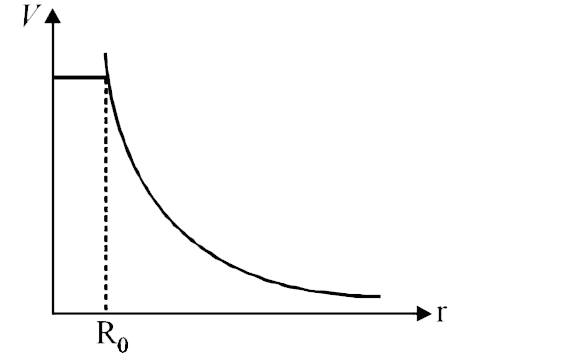
View SolutionFor spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View Solution
Knowledge Check
A spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
 A(a) Within r=2R0 total enclosed net charge is QB(b) Electric field is discontinued at r=R0C(c) Charge is only present at r=R0D(d) Electrostatic energy is zero for r<R0
A(a) Within r=2R0 total enclosed net charge is QB(b) Electric field is discontinued at r=R0C(c) Charge is only present at r=R0D(d) Electrostatic energy is zero for r<R0The electrostatic potential ϕr, of a spherical symmetrical system kept at origin, is shown in the adjacent figure, and given as
ϕr=q4πε0r(r≥R0)
ϕr=q4πε0R0(r≤R0)
Which of the following option is incorrect ?
 AFor spherical region r≤R0 total electrostatic energy stored is zeroBWith in r=2R0, total charge is q/2CThere will be no charge anywhere except at r = RDElectric field is discontinuous at r=R0
AFor spherical region r≤R0 total electrostatic energy stored is zeroBWith in r=2R0, total charge is q/2CThere will be no charge anywhere except at r = RDElectric field is discontinuous at r=R0The electrostatic potential (ϕr) of a spherical symmetric system , kept at origin is shown in the adhacent figure, and given as
ϕe=q4πɛ0r(r≤Ro)
ϕe=q4πɛ0Ro(r≤R0)

Which of the following option s in //are correct ?AFor spherical region r≤R0 total electrostatic energy stored id zero .BWithin r=2R0, total charge is q.CThere will be no charge anywhere except at r=R0.DElectric field is discontinuous at r=R0.
For spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View SolutionThe electrostatic potential ϕr, of a spherical symmetrical system kept at origin, is shown in the adjacent figure, and given as
ϕr=q4πε0r(r≥R0)
ϕr=q4πε0R0(r≤R0)
Which of the following option is incorrect ?

View SolutionIn a region of space having a spherical symmetic distribution of charge , the electric flux enclosed by a concentric spherical Gaussion surface, varies with radius
r as ϕ={ϕ0r2R3,r≤R<br>ϕ0, <R where R and ϕ0 are the constants.
View SolutionThe concentric, thin metallic spheres of radii r1 and r2(r1>r2) carry charges q1 and q2 respectively. Then the electric potential at distance r(r2<r<r1) will be 14πε0 times
View SolutionIn a region of space having a spherical symmetric distribution of charge , the electric flux enclosed by a concentric spherical Gaussian surface, varies with radius
r as ϕ={ϕ0r2R3,r≤R<br>ϕ0, <R where R and ϕ0 are the constants.
View Solution
