Three concentric metallic spherical shells of radii R , 2R 3R are given charges $Q_{1}, Q_{2}, Q_{3}$ respectively . It is found that the surface charge densities on the outer surfaces of the shells are equal . Then , the ratio of the charges given to the shells $Q_{1} : Q_{2} : Q_{3}$ is :

A

$1 : 2 : 3$

B

$1 : 3 : 5$

C

$1 : 4 : 9$

D

$1 : 8 : 18$

Text Solution

Verified by Experts

The correct Answer is:B

The charges on the surfaces of the metallic spheres are shown in the diagram . It is given that the surface charge densities on the outer surfaces of the shells are equal . Therefore ,

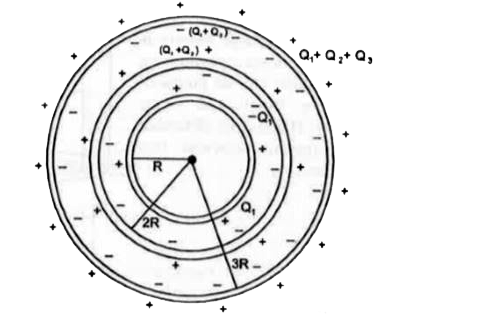
$\frac{Q_{1}}{4 π R^{2}} = \frac{Q_{1} + Q_{2}}{4 π {(2 R)}^{2}}$
$= \frac{Q_{1} + Q_{2} + Q_{3}}{4 π {(3 R)}^{2}} = x (s a y)$
$∴ Q_{1} = 4 π R^{2} x$
$Q_{1} + Q_{2} = 4 π {(2 R)}^{2} x = 4 [4 π R^{2} x]$
$\Rightarrow Q_{2} = 4 [4 π R^{2} x] - Q_{1}$
$= 4 [4 π R^{2} x] - 4 π R^{2} = 3 [4 π R^{2} x]$
Also
$Q_{1} + Q_{2} + Q_{3} = 4 π {(3 R)}^{2}$
$x = 9 [4 π R^{2} x]$
$: . Q_{3} = 9 [4 π R^{2} x] - Q_{1} - Q_{2}$
$= 9 [4 π R^{2} x] - 4 [4 π R^{2} x]$
$= 5 [4 π R^{2} x]$
$\Rightarrow Q_{1} : Q_{2} : Q_{3} = 1 : 3 : 5$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three concentric metallic spherical shells of radii R, 2R, 3R are given charges $Q_{1} Q_{2} Q_{3}$ , respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells $Q_{1} : Q_{2} : Q_{3}$ is
A $1 : 2 : 3$
B $1 : 3 : 5$
C $1 : 4 : 9$
D $1 : 8 : 18$
Question 2 - Select One
Two concentric spherical shells of radii R and 2R are given charges $Q_{1} and Q_{2}$ respectively.
The surfaces charge densities of the outer surfaces are equal. Determine the ratio $Q_{1} : Q_{2}$ .
A $1 : 2$
B $4 : 1$
C $1 : 4$
D $2 : 1$
Question 3 - Select One
There are three concentric metallic spherical shells of radii R, 2R and 3q, respectively. The middle spherical shell is connected to earth. Let $q_{1}$ be the charge appearing on the inner surface of the middle sphere and $q_{2}$ be the charge on outer surface of the middle sphere. Similarly $q_{3}$ is the charge appearing on inner surface of outermost sphere and $q_{4}$ is the charge appearing on outer surface of outermost sphere.

A $\begin{matrix} P & Q & R & S 4 & 3 & 1 & 2 \end{matrix}$
B $\begin{matrix} P & Q & R & S 4 & 3 & 2 & 1 \end{matrix}$
C $\begin{matrix} P & Q & R & S 3 & 4 & 1 & 2 \end{matrix}$
D $\begin{matrix} P & Q & R & S 3 & 4 & 2 & 1 \end{matrix}$

MODERN PUBLICATION-ELECTROSTATICS-LEVEL -II

Home
Ask Doubt
Profile