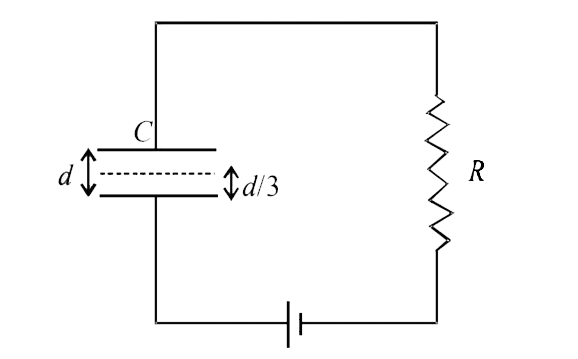
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K = 2 . The level of liquid is d/3 initially . Suppose the liquid level decreases at a constant speed v , the time constant as a function of time is :

A

$\frac{6 \in_{0} R}{5 d + 3 v t}$

B

$\frac{(15 d + 9 v t) ε_{0} R}{2 d^{2} - 3 d v t - 9 v^{2} t^{2}}$

C

$\frac{6 ε_{0} R}{5 d - 3 v t}$

D

$\frac{(15 d - 9 v t) ε_{0} R}{2 d^{2} - 3 d v t - 9 v^{2} t^{2}}$

Text Solution

Verified by Experts

The correct Answer is:A

Let the level of liquid at an instant of time .t. be x
Then $v = - \frac{d x}{d t} \Rightarrow d x = - v d t$
$\Rightarrow \int_{\frac{d}{3}}^{x} d x = v \int_{a}^{t} d t$
$\Rightarrow x - \frac{d}{3} = - v t$
$\Rightarrow x = \frac{d}{3} - v t$

Also , the capacitance can be considered as an equivalent of two capacitaces in seies such that
$\frac{1}{C_{e q}} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$
$\Rightarrow \frac{1}{C_{e q}} = \frac{1}{\frac{\in_{0} A}{d - x}} + \frac{1}{\frac{\in_{0} A K}{x}}$
$= \frac{d - x}{\in_{0} - A} + \frac{x}{\in_{0} A K}$
$∴ \frac{- 1}{C_{e q}} = \frac{- 1}{\in_{0} A} [\frac{d - x}{1} + \frac{x}{K}]$
$= \frac{1}{\in_{0} A} [\frac{K d - K x + x}{K}]$
$= \frac{K d + x (1 - K)}{\in_{0} A K}$
$∴ C_{e q} = \frac{\in_{0} A K}{k d + x (1 - K)}$
But A=1 , K = 2
and $x = \frac{d}{3} - v t$
$∴ C_{e q} = \frac{\in_{0} \times 1 \times 2}{2 d + [\frac{d}{3} - v t] (1 - 2)}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant $K = 2$ . The level of liquid is $d / 3$ initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-

A(a) $\frac{6 e π s l o n_{0} R}{5 d + 3 v t}$
B(b) $\frac{(15 d + 9 v t) ε_{0} R}{2 d^{2} - 3 d v t - 9 v^{2} t^{2}}$
C(c) $\frac{6 ε_{0} R}{5 d - 3 v t}$
D(d) $\frac{(15 d - 9 v t) ε_{0} R}{2 d^{2} - 3 d v t - 9 v^{2} t^{2}}$
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant $K_{1} = 6 and K_{2} = 4$ . New capacitance will be

A $4 \frac{A ε_{0}}{d}$
B $4.8 \frac{A ε_{0}}{d}$
C $5 \frac{A ε_{0}}{d}$
D $2.4 \frac{A ε_{0}}{d}$
A parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness $\frac{d}{2}$ and dielectric constants $\in_{1}$ and $\in_{2}$ respectively. The equivalent capacitance will be

A $\frac{\in_{0} A}{d} (\in_{1} + \in_{2})$
B $\frac{\in_{0} A}{d} \frac{(\in_{1} + \in_{2})}{\in_{1} \in_{2}}$
C $\frac{2 \in_{0} A}{d} \frac{\in_{1} \in_{2}}{(\in_{1} + \in_{2})}$
D $\frac{2 \in_{0} A}{d} \frac{(\in_{1} + \in_{2})}{\in_{1} \in_{2}}$

MODERN PUBLICATION-ELECTROSTATICS-LEVEL -II

Home
Ask Doubt
Profile