A liquid is kept in cylindrical vessel which is rotated along its axis . The liquid rises at the sides . If the radius of the vessel is m and the speed of rotation is 2 revper sec , find the difference in the height of the liquid at the centre of the vessel and at its sides
Consider a partical at position (x,y) as shown in figure .for its equilibrium along y - axis
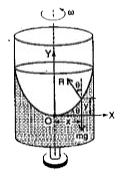
----------(i)
And for its circular motion in horizontal plane -------- (ii)
So , dividing Eqn . (ii) by (i) ---------(iii)
But from differential calculate that slope ------(iv)
So from Eqn . (iii) and (iv) i.e ,
which on the integration yields
But as at
---------(v)
Which is the equation of a parable .So , the surface of revolution is a paraboloid and for a point on the rim = h and x = r . So , ---------(vi)
Here , rad/s and r = 0.05 m
So , m = 2 cm
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View Solution
Knowledge Check
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cmA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2gA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
Arω2gBr2ω22gC√2grωDω22gr2
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionThe product of the numbers 5623 and 6 in the scale of eight is
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View Solution
