ABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that: ar(△BED)=14ar(△ABC)Solution in Punjabi
Step by step video & image solution for ABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that: ar(triangleBED) = 1/4 ar(triangleABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
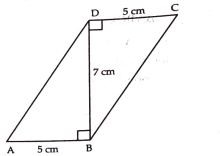 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

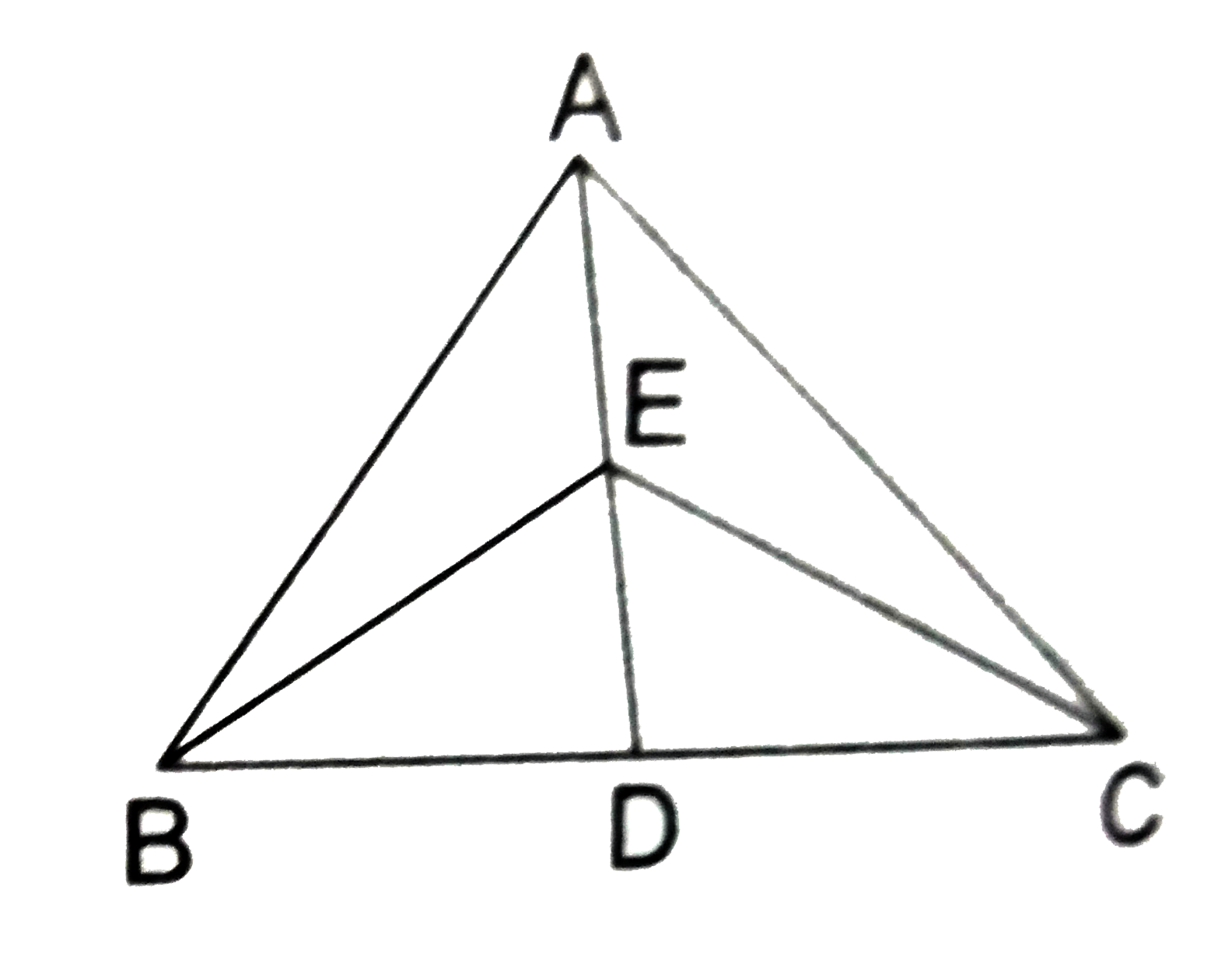
View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
View SolutionIn △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?

View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 14 ar (ABC).
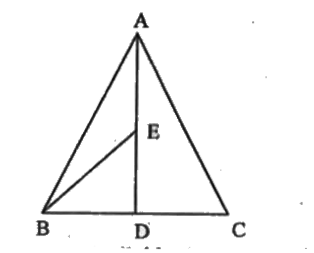
View SolutionIn a triangle ABC, E is the mid - point of median AD. Show that ar (BED) =1/4 ar (ABC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View SolutionIn △ABC, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=12ar(ABC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIf D, E, f are the mid-point of the sides of triangle ABC, prove that : ar(△DEF)=14ar(△ABC).
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (triangleBED)=1/4 ar( triangleABC ).
View SolutionD is the mid-point of side BC of Delta ABC and E is the mid-point of BO. If O is the mid-point of AE, then ar( Delta BOE) = 1/k ar( Delta ABC). Then k equals
View SolutionE is any point on median AD of a △ABC . Show that ar (ABE) = ar (ACE).
View SolutionD,E and F are mid-points of the sides BC, CA and AB respectively of triangleABC . Prove that ar(triangleDEF) = 1/4 ar (triangleABC)
View Solution
