Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
magnetic field is zero
magnetic field is 0.8 sqrt(0.8)mu""_0I/R
second derivative of magnetic field
first derivative of magnetic field dB/dx=0
The correct Answer is:B
Similar Questions
Consider two parallel co-axial circular coils of equal radius R, and number of turn N, carrying equal currents in the same direction and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B=0.72μ0NIR, approximately. [Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View Solution
Knowledge Check
Two identical coils are placed coaxially. They carry equal currents in same direction
NOTE in parts (a), (b) and (c) exclude the points at infinity.Aon their axis there are two points where net magnetic field is zeroBon their axis there are three points where net magnetic field is zeroCon their axis there is no such point where net magnetic field is zeroDon moving from the centre of one coil to the other, magnetic field will first decrease then increase
Two parallel coaxial circular coils of equal radius R and equal number of turns N carry equal currents I in the same direction and are separated by a distance 2R. Find the magnitude and direction of the net magnetic field produced at the mid-point of the line joining their centres.
View SolutionTwo identical coils having radius R and number of turns N are placed co-axially with their centres separated by a distance equal to their radius R. The two coils are given same current I in same direction. The configuration is often known as a pair of Helmholtz coil.
(i) Calculate the magnetic field (B) at a point (P) on the axis between the coils at a distance x from the centres of one of the coils.
(ii) Prove that dBdx=0 and d2Bdx2=0 [ In fact d3Bdx3 is also equal to zero ] at the point lying midway between the two coils. What conclusion can you draw from these results?

View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
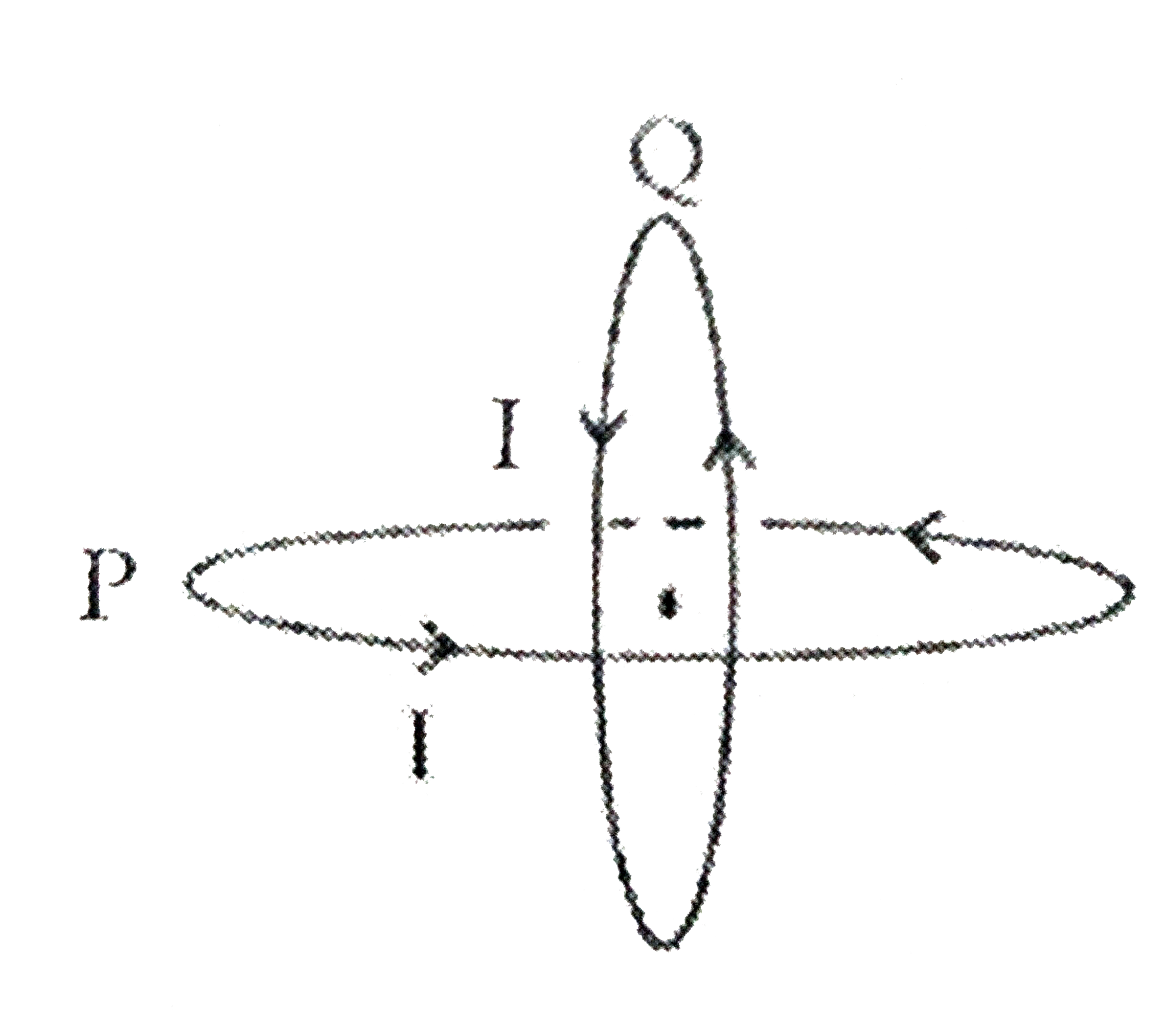
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.

View SolutionTwo identical circular coils, P and Q each of radius R, carrying currents 1 A and √3 A respectively, are placed concentrically are perpendicualr to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.

View SolutionTwo long straight wires are set parallel to each other Each carries a current i in the same direction and the separation between them is 2r. The intensity of the magnetic field midway between them is
View SolutionTwo identical coils are placed coaxially. They carry equal currents in same direction
NOTE in parts (a), (b) and (c) exclude the points at infinity.
View Solution
