A symmetric double convex lens is cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens was 4D, the power of a cut lens will be
A. 2D
B. 3D
C. 4D
D. 5D
The correct Answer is:A
To solve the problem, we need to determine the power of a cut lens when a symmetric double convex lens is cut into two equal parts. The power of the original lens is given as 4D (diopters).
1. Understand the Power of a Lens:
The power P of a lens is given by the formula:
P=1F
where F is the focal length of the lens.
2. Power of the Original Lens:
The power of the original double convex lens is given as P=4D.
3. Cutting the Lens:
When the lens is cut into two equal parts along a plane perpendicular to the principal axis, each half will behave like a new lens.
4. Analyzing the Cut Lens:
Each half of the lens will have a different effective focal length. The original lens has two curved surfaces, and when cut, one side will remain curved while the other side will become flat (plane surface).
5. Determine the New Radius of Curvature:
For the cut lens:
- The radius of curvature R1 of the curved surface remains R.
- The radius of curvature R2 of the flat surface is considered to be infinite (R2=∞).
6. Using the Lens Maker's Formula:
The power of the new lens (cut lens) can be calculated using the lens maker's formula:
P′=μ−1(1R1−1R2)
Substituting R1=R and R2=∞:
P′=μ−1(1R−0)=μ−1R
7. Relating to the Original Power:
From the original lens, we know:
P=μ−1(1R−(−1R))=2(μ−1)R
Since P=4D:
4=2(μ−1)R
Rearranging gives:
μ−1=4R2=2R
8. Substituting Back to Find New Power:
Now substituting μ−1=2R into the equation for P′:
P′=2RR=2D
9. Conclusion:
The power of each cut lens is 2D.
Final Answer:
The power of the cut lens will be 2D.
The power P of a lens is given by the formula:
P=1F
where F is the focal length of the lens.
The power of the original double convex lens is given as P=4D.
When the lens is cut into two equal parts along a plane perpendicular to the principal axis, each half will behave like a new lens.
Each half of the lens will have a different effective focal length. The original lens has two curved surfaces, and when cut, one side will remain curved while the other side will become flat (plane surface).
For the cut lens:
- The radius of curvature R1 of the curved surface remains R.
- The radius of curvature R2 of the flat surface is considered to be infinite (R2=∞).
The power of the new lens (cut lens) can be calculated using the lens maker's formula:
P′=μ−1(1R1−1R2)
Substituting R1=R and R2=∞:
P′=μ−1(1R−0)=μ−1R
From the original lens, we know:
P=μ−1(1R−(−1R))=2(μ−1)R
Since P=4D:
4=2(μ−1)R
Rearranging gives:
μ−1=4R2=2R
Now substituting μ−1=2R into the equation for P′:
P′=2RR=2D
The power of each cut lens is 2D.
The power of the cut lens will be 2D.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
78 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
A symmetric double convex lens is cut in two equal parts by a plane perpendiculr to the pricipal axis. If the power of the original lens was 4D, the power of a cut lens will be
a.2D b.3D c.4D d.5D
View SolutionIf a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
View SolutionA thin double convex lens is cut into two equal pieces A and B by a plane containing principal axis. The piece B is further cut into two more pieces pieces C and D by another plane perpendicular to the principal axis. If the focal power of the original lens is P, then thos of A and C are
View SolutionThe power of a lens is -5 D.
Name the type of lens.
View SolutionA thin, symmetric double convex lens of power P is cut into three parts A, B, and C as shown in Figure. The power of
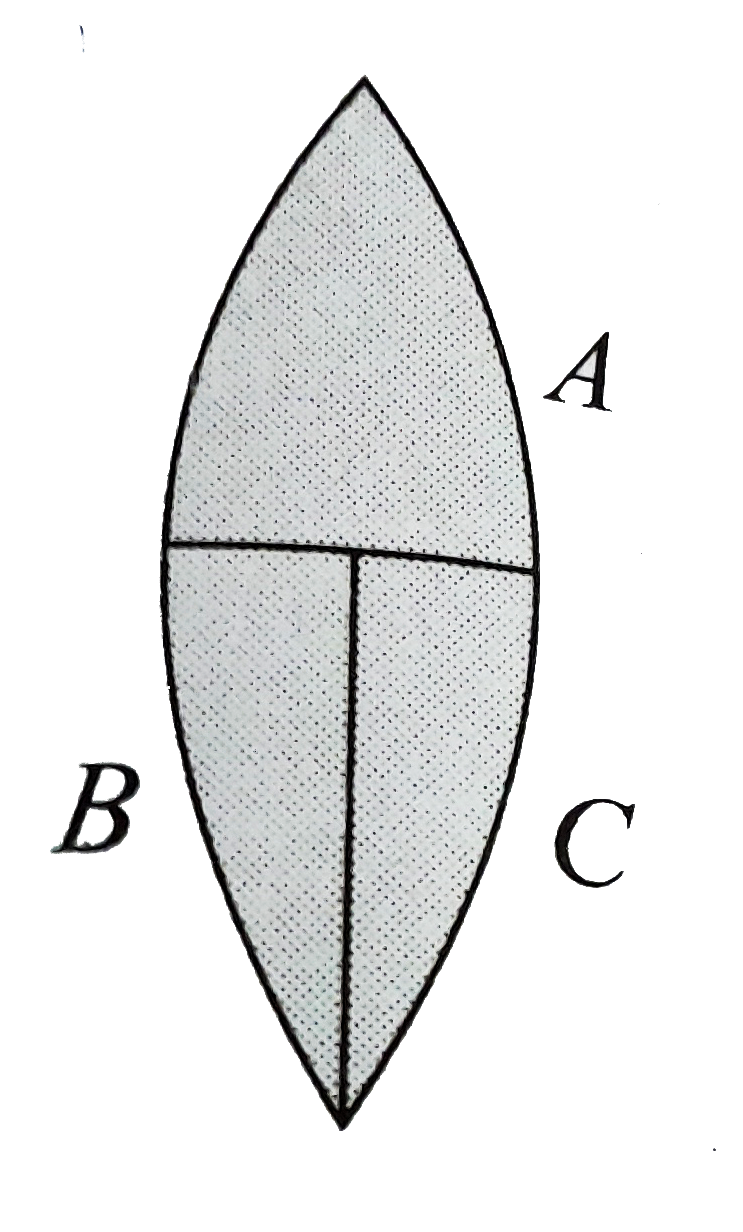
View SolutionThe two surfaces of a biconvex lens has same radii of curvatures . This lens is made of glass of refractive index 1.5 and has a focal length of 10 cm in air. The lens is cut into two equal halves along a plane perpendicular to its principal axis to yield two plane - convex lenses. The two pieces are glued such that the convex surfaces touch each other. If this combination lens is immersed in water (refractive index =43 ), its focal length (in cm ) is
View SolutionThe equiconvex lens has focal length f. If is cut perpendicular to the principal axis passin through optical centre, then focal length of each half is
View SolutionAn equiconvex lens of focal length20 cm is cut into two equal halves perpendicular to the principal axis and kept at a separation of 10 cm co-axially. What ils the focal length of the each part is?
View SolutionA thin symmetrical double convex lens of power P is cut into three parts, as shown in the figure. Power of A is

View SolutionA convex forms a real image of a poinnt object placed on its principal axis. If the upper half of the lens is painted black
View Solution
