A particle travels from point A to B on a circular path of radius 15/π cm.If the are length AB be 10 cm,find the displacement (figure)
To solve the problem, we need to find the displacement of a particle moving along a circular path from point A to point B, given the radius of the circular path and the arc length between the two points.
1. Identify the Given Values:
- Radius of the circular path, r=15π cm
- Arc length AB=10 cm
2. Relate Arc Length to Angle:
The arc length s is related to the radius r and the angle θ (in radians) by the formula:
s=r⋅θ
Here, the angle subtended at the center by the arc length AB is 2θ (since we have two angles of θ at points A and B).
3. Set Up the Equation:
Using the arc length formula:
10=(15π)⋅2θ
Simplifying this gives:
10=30θπ
4. Solve for θ:
Rearranging the equation to solve for θ:
θ=10π30=π3 radians
5. Convert θ to Degrees:
Since θ is often more useful in degrees for geometric calculations:
θ=60∘
6. Use Right Triangle to Find Displacement:
The displacement d between points A and B can be found using the formula for the length of the chord in a circle:
d=2rsin(θ2)
Here, θ2=30∘.
7. Calculate d:
Substituting the values:
d=2(15π)sin(30∘)
Since sin(30∘)=12:
d=2(15π)⋅12=15π cm
Final Answer:
The displacement from point A to point B is:
15π cm
---
- Radius of the circular path, r=15π cm
- Arc length AB=10 cm
The arc length s is related to the radius r and the angle θ (in radians) by the formula:
s=r⋅θ
Here, the angle subtended at the center by the arc length AB is 2θ (since we have two angles of θ at points A and B).
Using the arc length formula:
10=(15π)⋅2θ
Simplifying this gives:
10=30θπ
Rearranging the equation to solve for θ:
θ=10π30=π3 radians
Since θ is often more useful in degrees for geometric calculations:
θ=60∘
The displacement d between points A and B can be found using the formula for the length of the chord in a circle:
d=2rsin(θ2)
Here, θ2=30∘.
Substituting the values:
d=2(15π)sin(30∘)
Since sin(30∘)=12:
d=2(15π)⋅12=15π cm
The displacement from point A to point B is:
15π cm
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)22videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)29videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE58videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
Similar Questions
A particle travels from A to B path shown in figure, then the displacement of particle is :
 .View Solution
.View SolutionThree particles P, Q and R
are situated at point A on the circular path of radius 10m. All three particles move along different path and reach at point B shown in figure. Then the ratio of distance traversed by particle P and Q is:-
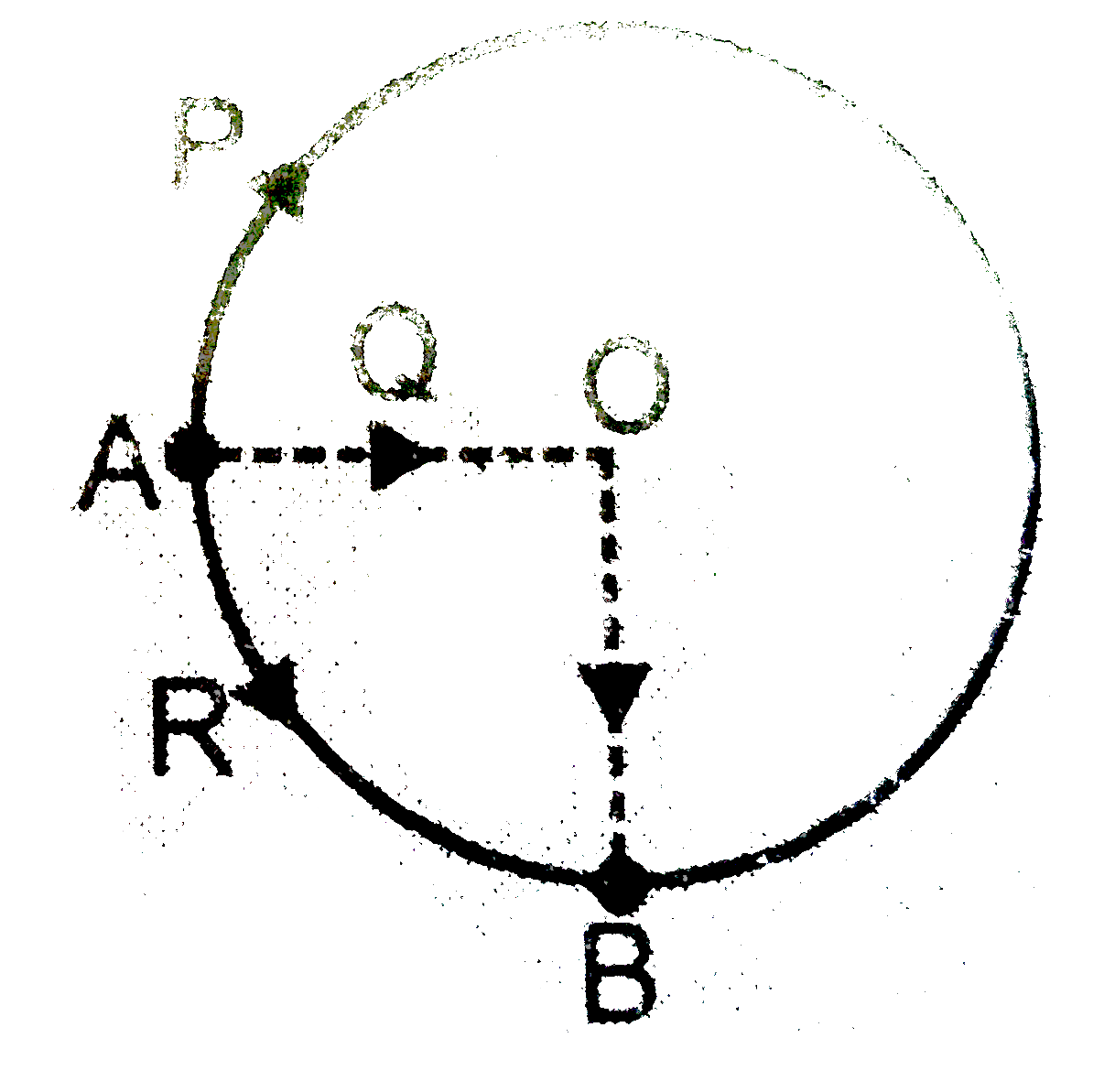 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
Displacement of a person moving from A to B along a semicircular path of radius R is 100 m. What is the distance travelled by him ?
View SolutionA particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
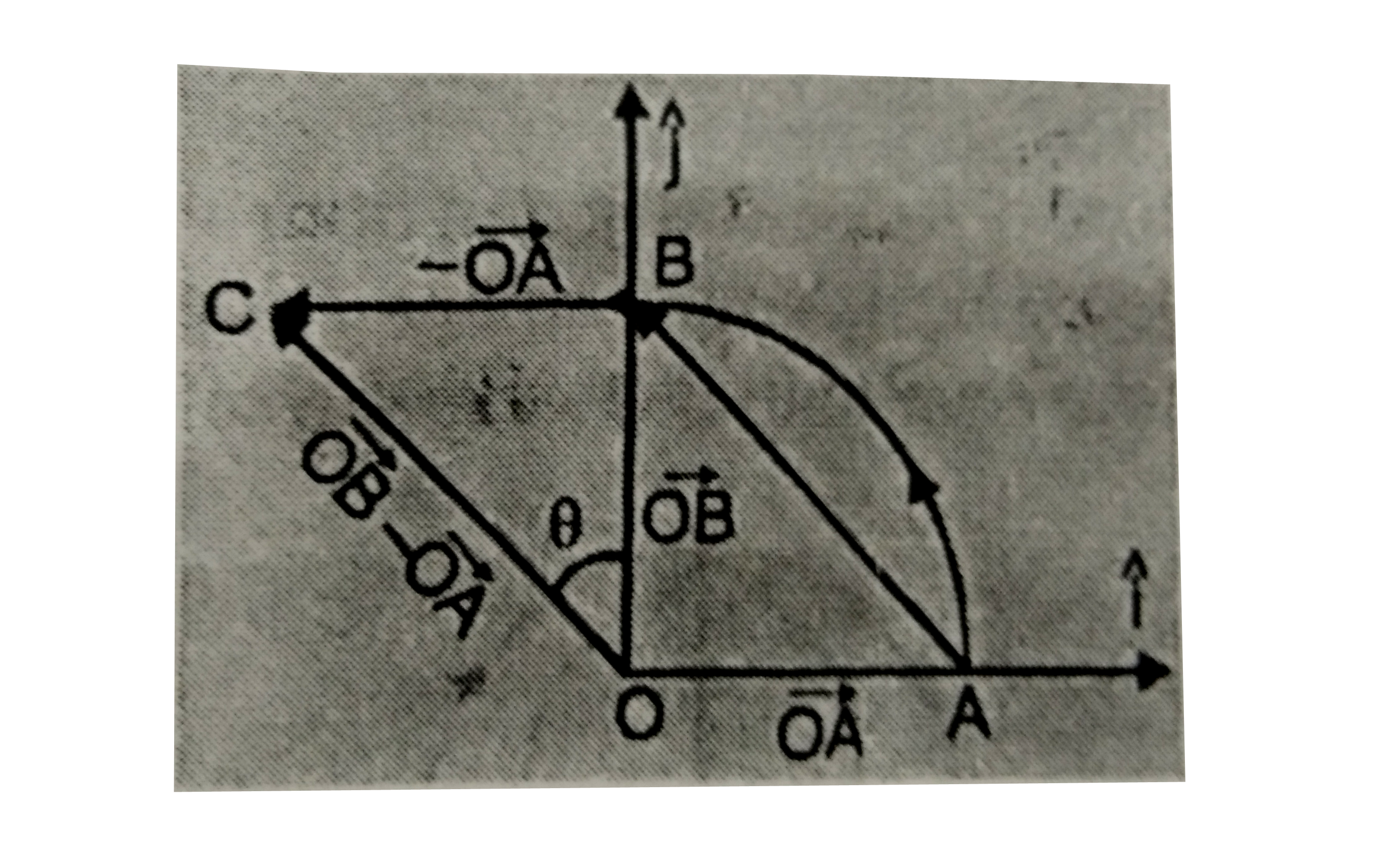 View Solution
View SolutionA wave travelling on a string at a speed of 10ms−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave ? (b) If the displacement of a particle is 1.5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant ?
View SolutionThe tangential acceleration of a particle moving in a circular path of radius 5cm is 2ms−2. The angular velocity of the particle increases from 10rads−1 to 20rads−1 during some time. Find
(a) this duration od time and
(b) the number of revolutions completed during this time.View SolutionA particle moves in a circular path of radius 5 cm in a plane perpendicular to the principla axis of a xonvex mirror with radius of curvature 20cm. The object is 15cm in front of the mirror. Calculate the radius of the circular path of the image.
View SolutionA particle travels along the path ABC, as shown in the figure given below, AB = BC = l, calculate the path length and displacement of the particle
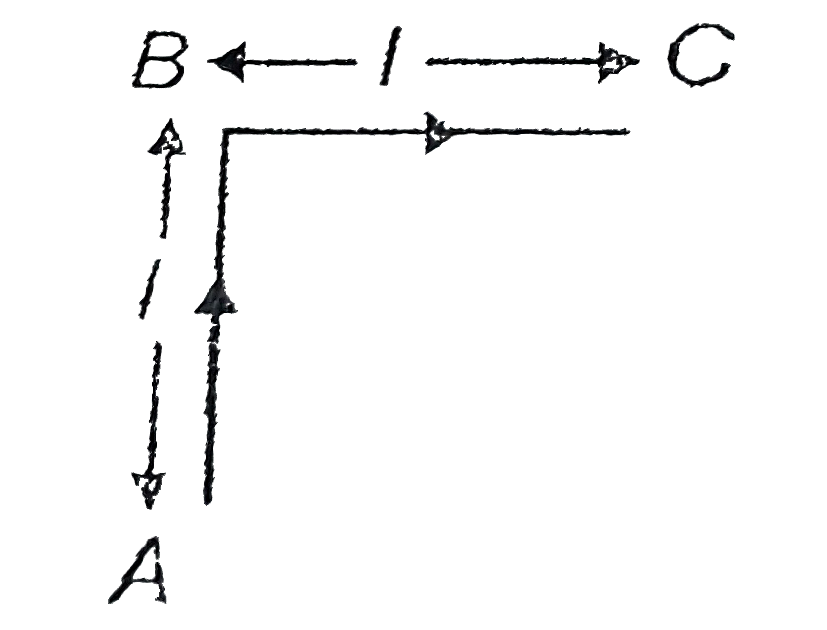 View Solution
View SolutionA particle moves along a circular path of radius R. The distance and displacement of a particle after one completer revolution is
View Solution

