Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
Squating the given equation ,we get v2=4+4s
Now,Comparing it with v2=u2+2as
We get,u=2m/s and a=2 m/ s2
Therefore,Displacement t=2s is
S=ut+12at2 or s=(2)(2)2 or s=8 m
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)22videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)29videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE58videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
Similar Questions
Velocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
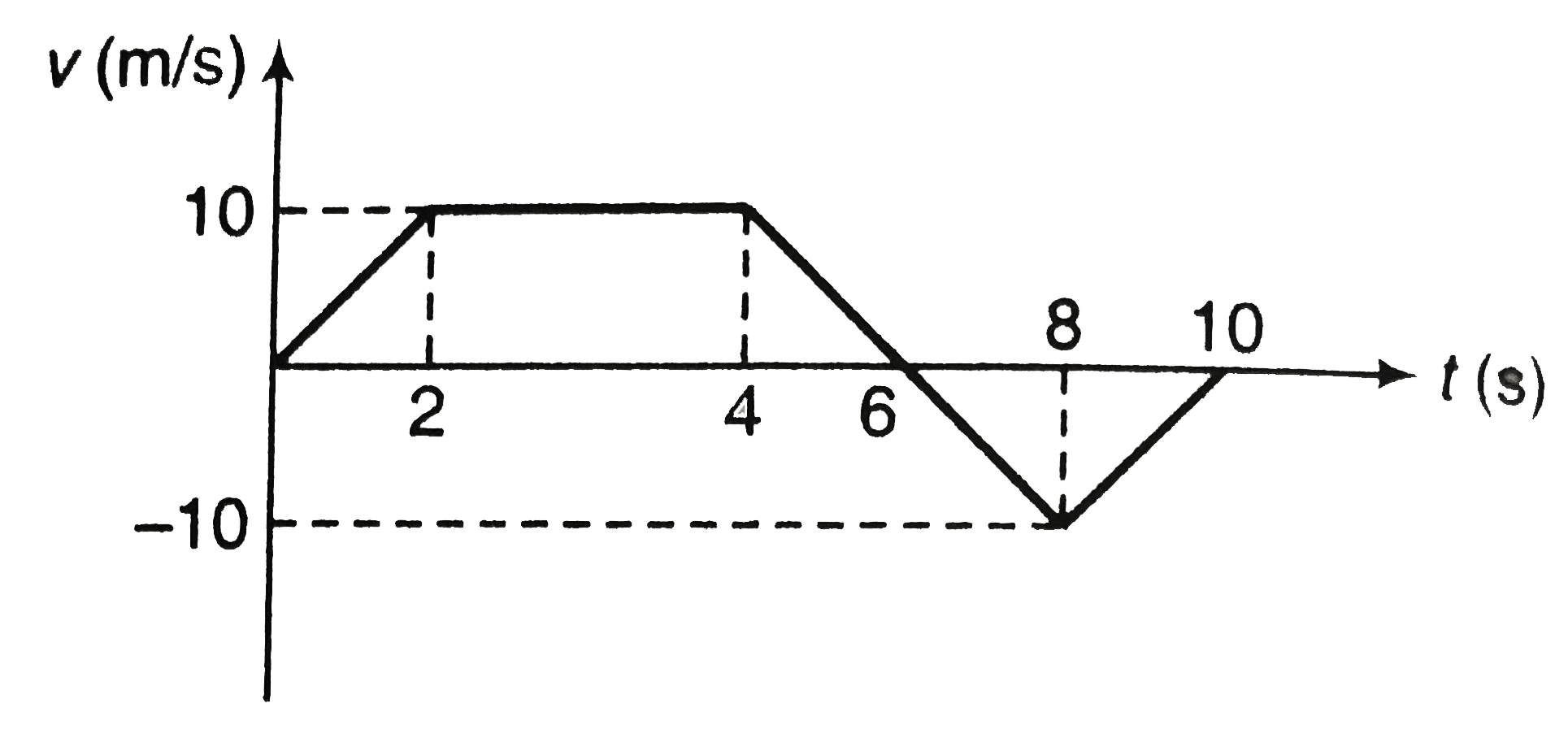
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8sView SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
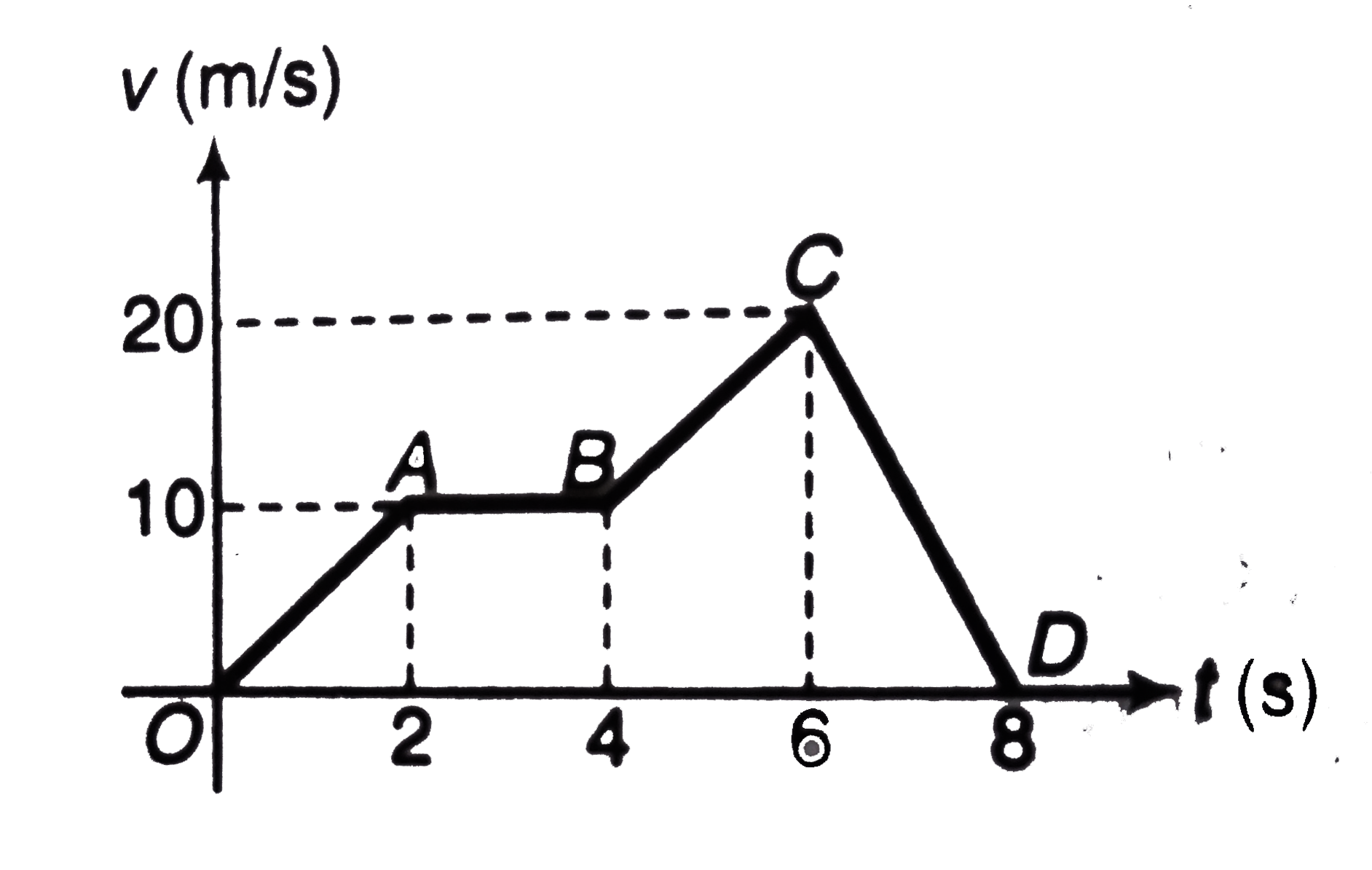 View Solution
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
 View Solution
View SolutionThe acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
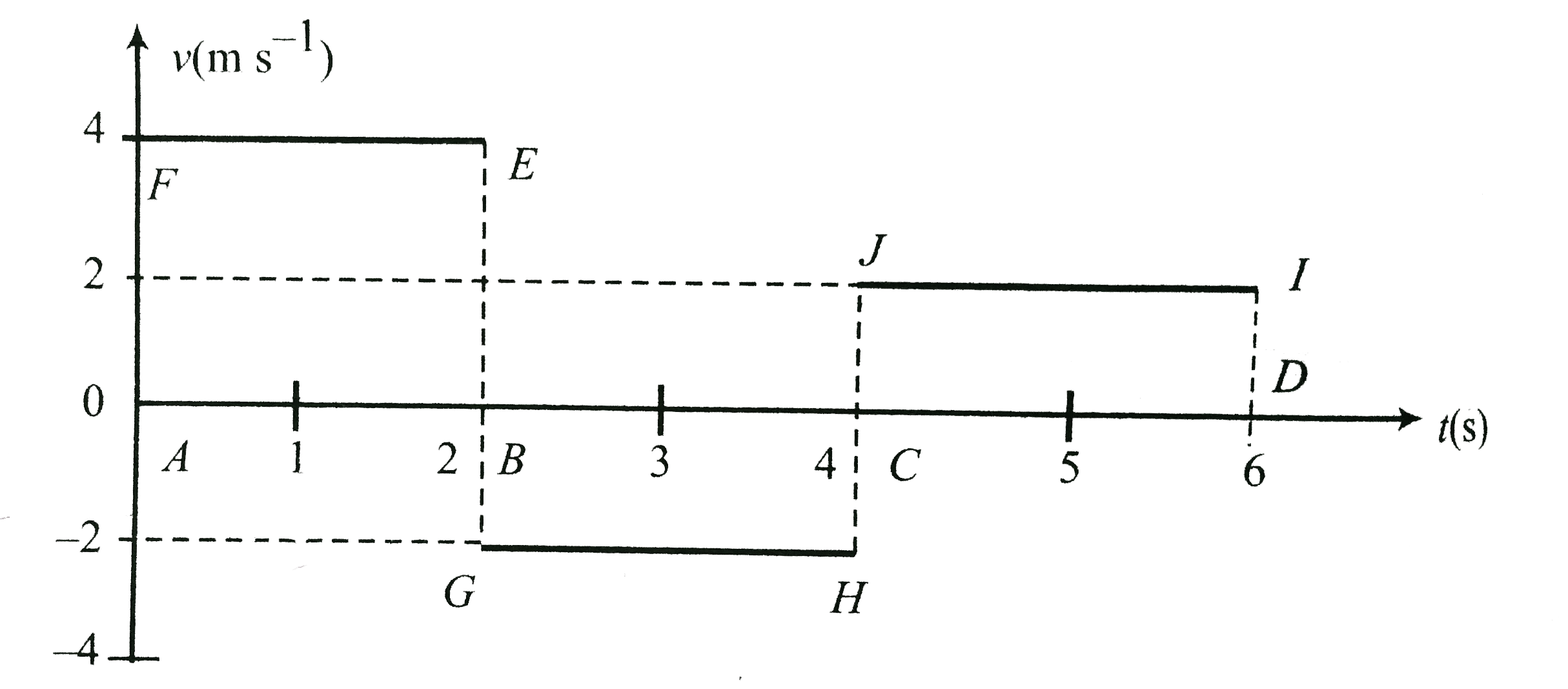 .View Solution
.View SolutionVelocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3sView SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
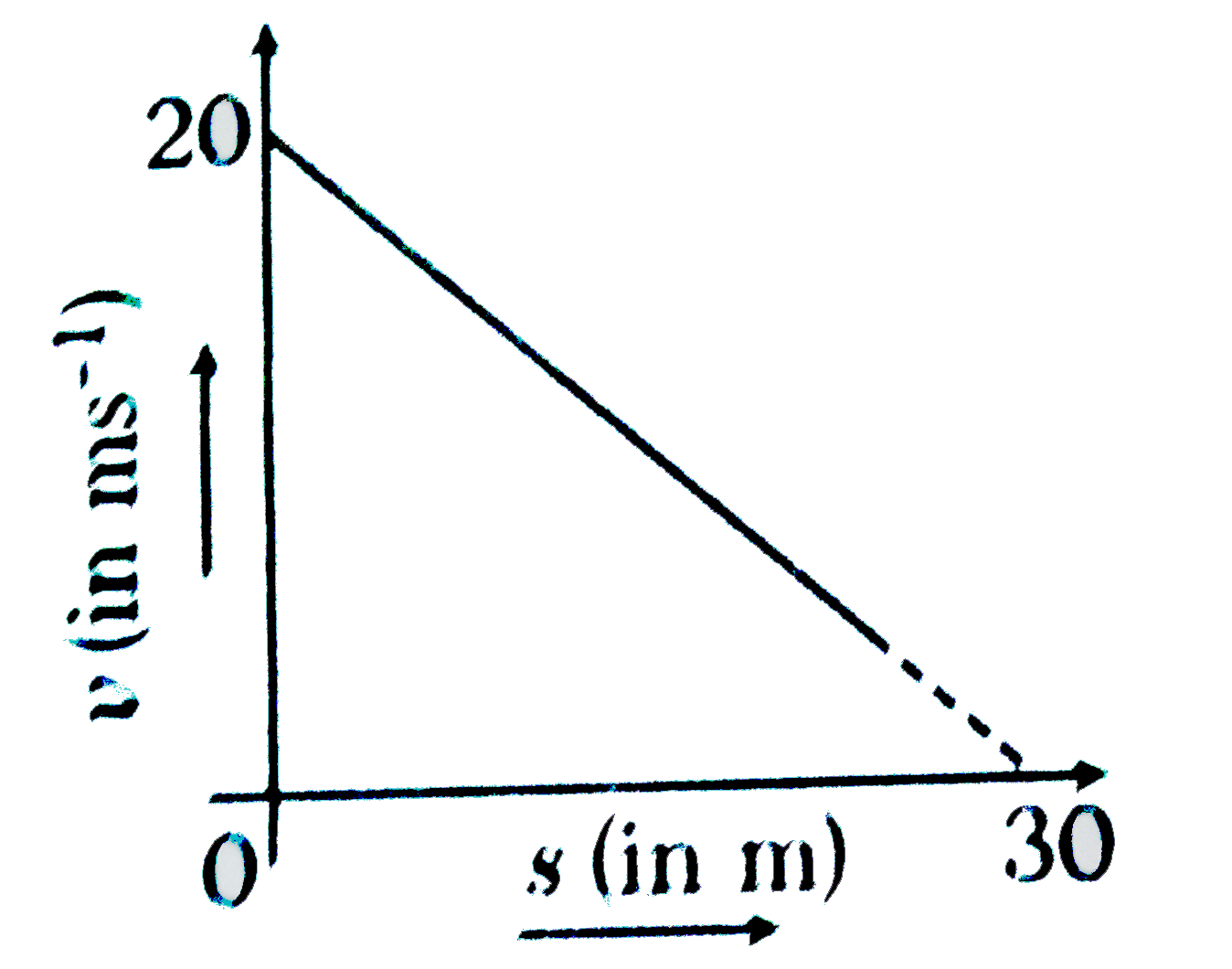 View Solution
View Solution

