Each side of ΔABC is the polar of the opposite vertex with respect to a circle with centre P. Then P is ortho centre of ΔABC.
The correct Answer is:the circle
To prove that point P is the orthocenter of triangle ABC when each side of triangle ABC is the polar of the opposite vertex with respect to a circle with center P, we can follow these steps:
Step 1: Understand the Definitions
- Polar of a Point: The polar of a point with respect to a circle is the locus of points where tangents drawn from the point to the circle are perpendicular to the radius at the point of tangency.
- Orthocenter: The orthocenter of a triangle is the point where the three altitudes intersect.
Step 2: Identify the Polar Relationships
Let’s denote the sides of triangle ABC as follows:
- Side BC is the polar of vertex A.
- Side AC is the polar of vertex B.
- Side AB is the polar of vertex C.
Step 3: Establish the Polar Condition
Since each side of triangle ABC is the polar of the opposite vertex with respect to the circle centered at P, we can write:
- The point A lies on the polar of A, which is line BC.
- The point B lies on the polar of B, which is line AC.
- The point C lies on the polar of C, which is line AB.
Step 4: Use the Properties of Polars
From the properties of polars, we know that if a point lies on the polar of another point, the line connecting these two points is perpendicular to the line connecting the center of the circle to the point on the polar.
Step 5: Establish Perpendicularity
1. Since A lies on the polar of A (line BC), the line AP is perpendicular to line BC.
2. Since B lies on the polar of B (line AC), the line BP is perpendicular to line AC.
3. Since C lies on the polar of C (line AB), the line CP is perpendicular to line AB.
Step 6: Conclude the Position of P
Since P is the point from which the perpendiculars to the sides of triangle ABC are drawn, P must be the intersection point of the altitudes of triangle ABC. Therefore, P is the orthocenter of triangle ABC.
Final Conclusion
Thus, we have shown that if each side of triangle ABC is the polar of the opposite vertex with respect to a circle centered at P, then P is indeed the orthocenter of triangle ABC.
---
- Polar of a Point: The polar of a point with respect to a circle is the locus of points where tangents drawn from the point to the circle are perpendicular to the radius at the point of tangency.
- Orthocenter: The orthocenter of a triangle is the point where the three altitudes intersect.
Let’s denote the sides of triangle ABC as follows:
- Side BC is the polar of vertex A.
- Side AC is the polar of vertex B.
- Side AB is the polar of vertex C.
Since each side of triangle ABC is the polar of the opposite vertex with respect to the circle centered at P, we can write:
- The point A lies on the polar of A, which is line BC.
- The point B lies on the polar of B, which is line AC.
- The point C lies on the polar of C, which is line AB.
From the properties of polars, we know that if a point lies on the polar of another point, the line connecting these two points is perpendicular to the line connecting the center of the circle to the point on the polar.
1. Since A lies on the polar of A (line BC), the line AP is perpendicular to line BC.
2. Since B lies on the polar of B (line AC), the line BP is perpendicular to line AC.
3. Since C lies on the polar of C (line AB), the line CP is perpendicular to line AB.
Since P is the point from which the perpendiculars to the sides of triangle ABC are drawn, P must be the intersection point of the altitudes of triangle ABC. Therefore, P is the orthocenter of triangle ABC.
Thus, we have shown that if each side of triangle ABC is the polar of the opposite vertex with respect to a circle centered at P, then P is indeed the orthocenter of triangle ABC.
Similar Questions
Each side of ΔABC is the polarof the opposite vertex with respect to a circle with centre P. For the ΔABC the point P is
View SolutionThe polar of p with respect to a circle s=x2+y2+2gx+2fy+c=0 with centre C is
View Solution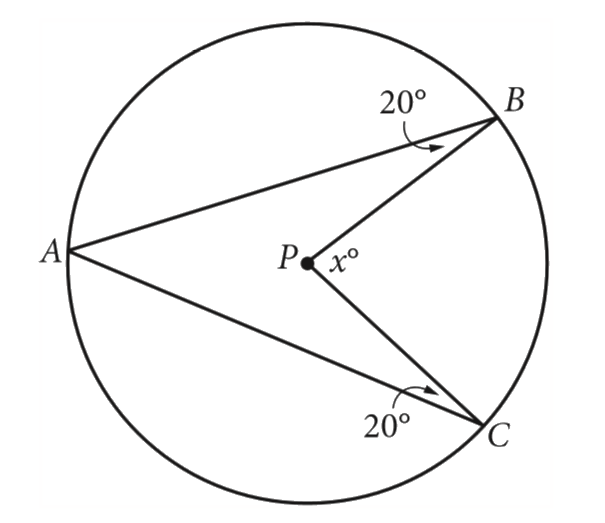
Point P is the centre of the circle in the figure above. What is the value of x?
View SolutionThe equations of the sides AB and CA of a ΔABC are x+2y=0 and x−y=3 respectively. Given a fixed point P(2, 3).
Q. If P be orthocentre of ΔABC then equation of side BC is :
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
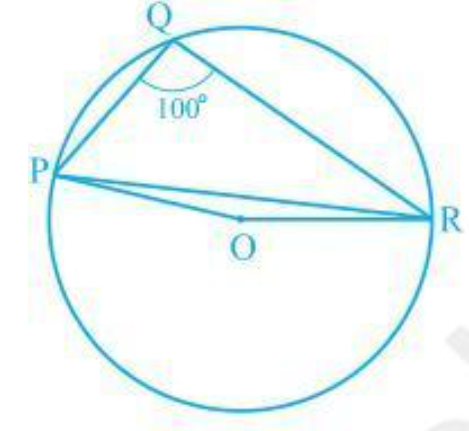
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionLet the equations of perpendicular bisectors of sides ACandofΔABCbex+y=3andx−y=1 respectively Then vertex A is is (0,0)
The orthocentre of ΔABC is
View SolutionLet the equations of perpendicular bisectors of sides ACandABofΔABCisx+y=3andx−y=1 respectively Then vertex A is is (0,0)
The circumcentre of the ΔABC is
View SolutionIf in a ΔABC, the altitudes from the vertices A, B, C on opposite sides are in H.P, then sin A, sin B, sin C are in
View Solution
