Question

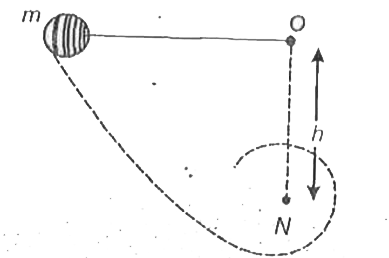
A particle of mass 'm' is attached to one end of a string of length 'l' while the other end is fixed to a point 'h' above the horizontal table, the particle is made to revolve in a circle on the table, so as to make P revolution per sec. The maximum value of P if the particle is to be contact with the table is

Options

A. `2pisqrt(gh)`
B. `sqrt((g)/(h))`
C. `2pisqrt((h)/(g))`
D. `(1)/(2pi)sqrt((g)/(h))`

Answer

D

Explanation

To solve the problem, we need to analyze the forces acting on the particle as it revolves in a horizontal circle while being attached to a string fixed at a height above the table. Here's a step-by-step breakdown of the solution:

Step 1: Understand the Setup
We have a particle of mass \( m \) attached to a string of length \( l \). The other end of the string is fixed at a height \( h \) above the horizontal table. The particle revolves in a horizontal circle, and we need to find the maximum frequency \( P \) (in revolutions per second) at which the particle can revolve while remaining in contact with the table.

Step 2: Identify Forces Acting on the Particle
When the particle is in circular motion, the following forces are acting on it:
1. Tension (T) in the string, acting towards the center of the circle.
2. Weight (mg) of the particle, acting downwards.
3. Normal force (N) from the table, acting upwards.

Step 3: Analyze the Forces
For the particle to remain in contact with the table, the normal force \( N \) must be zero at the maximum frequency. Thus, we can set up the following equations based on the forces:

1. In the vertical direction:
\( T \cos \theta = mg \)
where \( \theta \) is the angle between the string and the vertical.

2. In the horizontal direction (providing the centripetal force):
\( T \sin \theta = m \frac{v^2}{r} \)
where \( r \) is the horizontal radius of the circular path.

Step 4: Relate \( \theta \) to \( h \) and \( l \)
Using the geometry of the situation:
\( \sin \theta = \frac{r}{l} \quad \text{and} \quad \cos \theta = \frac{h}{l} \)
From the right triangle formed by the string, height, and radius, we can express \( r \) as:
\( r = \sqrt{l^2 - h^2} \)

Step 5: Substitute \( T \) from Vertical Force Equation
From the vertical force equation, we can express the tension \( T \):
\( T = \frac{mg}{\cos \theta} = \frac{mg l}{h} \)

Step 6: Substitute \( T \) into the Horizontal Force Equation
Now substituting \( T \) into the horizontal force equation:
\( \frac{mg l}{h} \sin \theta = m \frac{v^2}{r} \)
Substituting \( \sin \theta = \frac{r}{l} \):
\( \frac{mg l}{h} \cdot \frac{r}{l} = m \frac{v^2}{r} \)
This simplifies to:
\( \frac{mg r}{h} = m \frac{v^2}{r} \)
Cancelling \( m \) and rearranging gives:
\( v^2 = \frac{g r^2}{h} \)

Step 7: Relate Linear Velocity to Angular Velocity
The linear velocity \( v \) is related to the angular velocity \( \omega \) by:
\( v = r \omega \)
Substituting this into the equation gives:
\( (r \omega)^2 = \frac{g r^2}{h} \)
This simplifies to:
\( \omega^2 = \frac{g}{h} \)

Step 8: Convert Angular Velocity to Frequency
The frequency \( P \) in revolutions per second is related to the angular velocity \( \omega \) by:
\( P = \frac{\omega}{2\pi} \)
Substituting \( \omega = \sqrt{\frac{g}{h}} \):
\( P = \frac{1}{2\pi} \sqrt{\frac{g}{h}} \)

Final Answer
Thus, the maximum value of \( P \) is:
\( P = \frac{1}{2\pi} \sqrt{\frac{g}{h}} \)