Two identical pendulums A and B are suspended from the same point. Both are given positive charge, with A having more charge than B. They diverge and reach equilibrium with the suspension of A and B making angles θ1andθ2 with the vertical respectively.
θ1>θ2
θ1<θ2
θ1=θ2
The tension in A is greater than that in B
The correct Answer is:C
To solve the problem of two identical pendulums A and B that are given positive charges and reach equilibrium at angles θ₁ and θ₂ with the vertical, we can analyze the forces acting on each pendulum and their equilibrium conditions.
1. Identify the Forces Acting on Each Pendulum:
- Each pendulum experiences three main forces:
- The gravitational force (weight) acting downwards: mg
- The tension in the string acting along the string: T
- The electrostatic force due to the repulsion between the two charged pendulums.
2. Analyze the Electrostatic Force:
- Since both pendulums are positively charged, they will repel each other. Let the charge on pendulum A be qA and the charge on pendulum B be qB, with qA>qB.
- The electrostatic force F between the two charges can be expressed using Coulomb's Law:
F=kqAqBr2
where k is Coulomb's constant and r is the distance between the two charges.
3. Set Up the Equilibrium Conditions:
- In equilibrium, the forces acting on each pendulum must balance. For pendulum A, we can resolve the forces into components:
- Vertical component: Tcos(θ1)=mg
- Horizontal component: Tsin(θ1)=F
- For pendulum B, similarly:
- Vertical component: Tcos(θ2)=mg
- Horizontal component: Tsin(θ2)=F′ (where F′ is the electrostatic force acting on B).
4. Relate the Angles and Forces:
- Since both pendulums are identical and experience the same gravitational force, the tension T in the strings will be the same when they are at equilibrium.
- Therefore, from the vertical force balance, we have:
Tcos(θ1)=mgandTcos(θ2)=mg
- This implies that cos(θ1)=cos(θ2), leading to θ1=θ2 if the angles are small.
5. Conclusion:
- Since pendulum A has a greater charge than pendulum B, it will experience a greater electrostatic force, causing it to diverge more than pendulum B. However, the equilibrium conditions imply that the angles will be equal due to the identical nature of the pendulums and the balancing of forces.
- Therefore, we conclude that:
θ1=θ2
Final Answer:
The angles θ1 and θ2 made by pendulums A and B with the vertical are equal, i.e., θ1=θ2.
- Each pendulum experiences three main forces:
- The gravitational force (weight) acting downwards: mg
- The tension in the string acting along the string: T
- The electrostatic force due to the repulsion between the two charged pendulums.
- Since both pendulums are positively charged, they will repel each other. Let the charge on pendulum A be qA and the charge on pendulum B be qB, with qA>qB.
- The electrostatic force F between the two charges can be expressed using Coulomb's Law:
F=kqAqBr2
where k is Coulomb's constant and r is the distance between the two charges.
- In equilibrium, the forces acting on each pendulum must balance. For pendulum A, we can resolve the forces into components:
- Vertical component: Tcos(θ1)=mg
- Horizontal component: Tsin(θ1)=F
- For pendulum B, similarly:
- Vertical component: Tcos(θ2)=mg
- Horizontal component: Tsin(θ2)=F′ (where F′ is the electrostatic force acting on B).
- Since both pendulums are identical and experience the same gravitational force, the tension T in the strings will be the same when they are at equilibrium.
- Therefore, from the vertical force balance, we have:
Tcos(θ1)=mgandTcos(θ2)=mg
- This implies that cos(θ1)=cos(θ2), leading to θ1=θ2 if the angles are small.
- Since pendulum A has a greater charge than pendulum B, it will experience a greater electrostatic force, causing it to diverge more than pendulum B. However, the equilibrium conditions imply that the angles will be equal due to the identical nature of the pendulums and the balancing of forces.
- Therefore, we conclude that:
θ1=θ2
The angles θ1 and θ2 made by pendulums A and B with the vertical are equal, i.e., θ1=θ2.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-II
56 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assess Your Self
13 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
Two positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
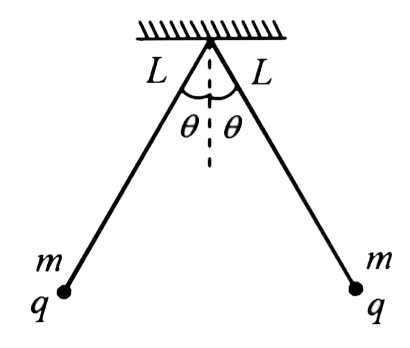
View SolutionTwo identical small equally charged conducting balls are suspended from long threads secured at one point. The charges and masses of the balls are such that they are in equilibrium when the distance between them is a(the length of thread L>>a). Then one of the balls is discharged. what will be the distance b(b<<L) between the balls when equilibrium is restored?
View SolutionTwo identical charged spheres of material density ρ, suspended from the same point by inextensible strings of equal length make an angle θ between the string. When suspended in a liquid of density σ the angle θ remains the same. The dielectric constant K of the liquid is
View SolutionThe net field →E due to the uniformly charged rod at P makes angles θ1 and θ2 with AP and BP respectively. Then find the value of θ1/θ2

View SolutionTwo identical capacitors A and B are charged to the same potential and then made to discharge through resistances RA and RB respectively, with RA>RB.
View SolutionFour pendulums A, B, C and D are suspended from the same

elastic support as shown in figure. A and C are of the same length, while B is smaller than A and D is larger than A. If A is given a transverse displacement,
View SolutionFour pendulums A,B,C and D are suspended from the same elastic support as shown in figure. A and C are of the same length , while B is smaller thatn A and D is larger than A. If A is given a transverse displacement,
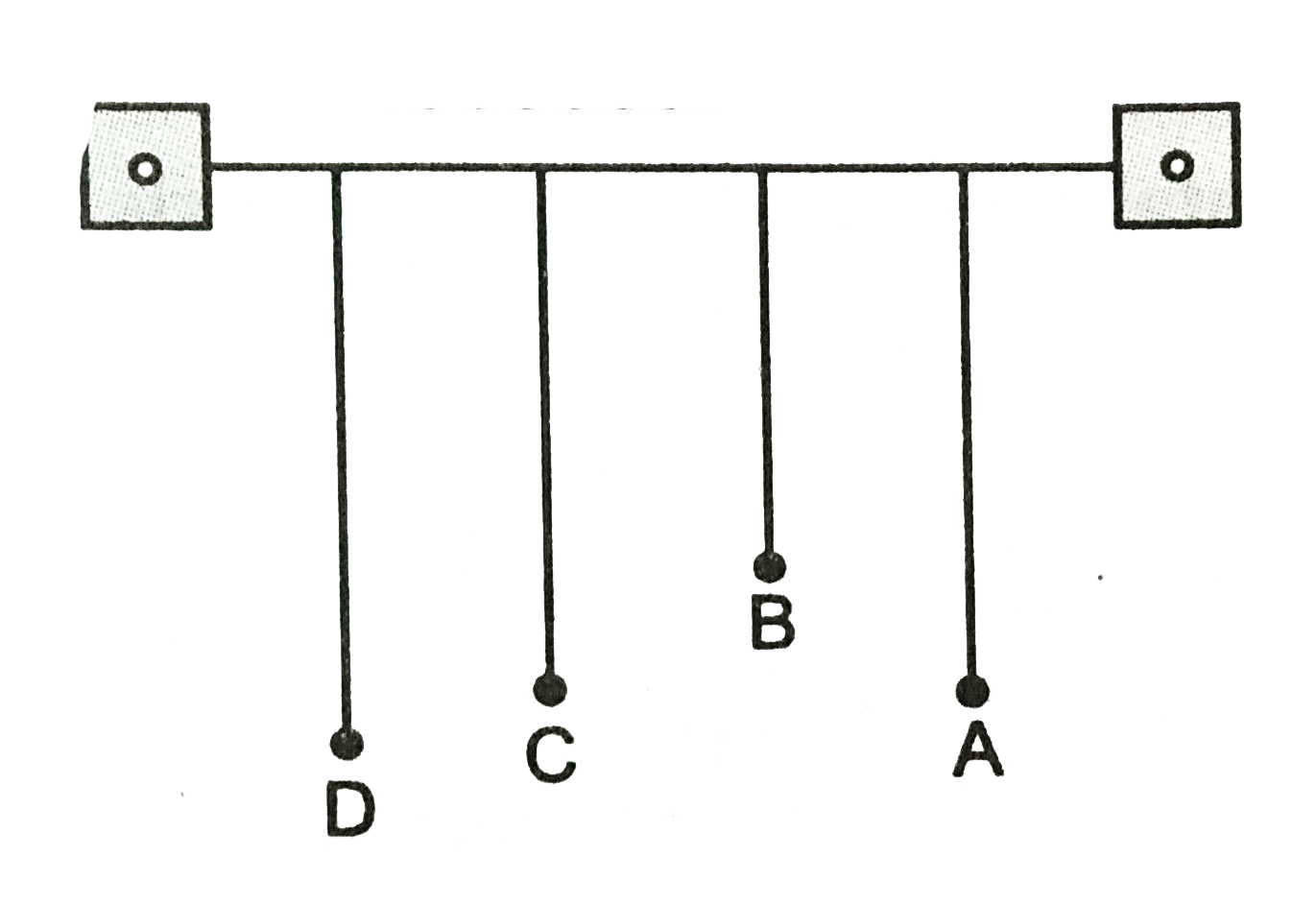
View Solution
