Show that the distance between a real object and its real image formed by a thin converging lens is always greater than or equal to four times the focal length of the lens.
To show that the distance between a real object and its real image formed by a thin converging lens is always greater than or equal to four times the focal length of the lens, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula for a thin lens is given by:
1f=1v−1u
where:
- f is the focal length of the lens,
- v is the image distance (positive for real images),
- u is the object distance (negative for real objects).
Step 2: Define the Distances
Let:
- d be the distance between the object and the image,
- x be the distance of the image from the lens,
- Therefore, the object distance u can be expressed as u=−(d−x).
Step 3: Substitute into the Lens Formula
Substituting u into the lens formula gives:
1f=1x−1−(d−x)
This simplifies to:
1f=1x+1d−x
Step 4: Find a Common Denominator
Combining the fractions on the right-hand side:
1f=(d−x)+xx(d−x)=dx(d−x)
Thus, we can rearrange this to find:
f=x(d−x)d
Step 5: Rearrange to Form a Quadratic Equation
Multiplying both sides by d gives:
fd=x(d−x)
Rearranging this leads to:
x2−dx+fd=0
Step 6: Apply the Discriminant Condition
For x to have real values, the discriminant of this quadratic equation must be non-negative:
D=b2−4ac≥0
Here, a=1, b=−d, and c=fd:
(−d)2−4(1)(fd)≥0
This simplifies to:
d2−4fd≥0
Step 7: Factor the Inequality
Factoring gives:
d(d−4f)≥0
This inequality holds true if either:
1. d≥4f (since d must be positive for real objects and images),
2. or d=0 (which is not a practical case).
Conclusion
Thus, we conclude that:
d≥4f
This shows that the distance between a real object and its real image formed by a thin converging lens is always greater than or equal to four times the focal length of the lens.
---
The lens formula for a thin lens is given by:
1f=1v−1u
where:
- f is the focal length of the lens,
- v is the image distance (positive for real images),
- u is the object distance (negative for real objects).
Let:
- d be the distance between the object and the image,
- x be the distance of the image from the lens,
- Therefore, the object distance u can be expressed as u=−(d−x).
Substituting u into the lens formula gives:
1f=1x−1−(d−x)
This simplifies to:
1f=1x+1d−x
Combining the fractions on the right-hand side:
1f=(d−x)+xx(d−x)=dx(d−x)
Thus, we can rearrange this to find:
f=x(d−x)d
Multiplying both sides by d gives:
fd=x(d−x)
Rearranging this leads to:
x2−dx+fd=0
For x to have real values, the discriminant of this quadratic equation must be non-negative:
D=b2−4ac≥0
Here, a=1, b=−d, and c=fd:
(−d)2−4(1)(fd)≥0
This simplifies to:
d2−4fd≥0
Factoring gives:
d(d−4f)≥0
This inequality holds true if either:
1. d≥4f (since d must be positive for real objects and images),
2. or d=0 (which is not a practical case).
Thus, we conclude that:
d≥4f
This shows that the distance between a real object and its real image formed by a thin converging lens is always greater than or equal to four times the focal length of the lens.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )53videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)57videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (LONG ANSWER QUESTIONS )9videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions

The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will beView SolutionThe minimum distance between an object and its real image formed by a convex lens is
View SolutionThe minimum distance between a real object and its real image formed by a thin converging lens of focal length f is
View SolutionThe minimum distance between an object and its real image formed by a thin convex lens of focal length f is K.f. Find the value of K.
View SolutionThe distance between the object and its real image from the convex lens is 60 cm and the height of image is two times the height of object . The focal length of the lens is
View SolutionChoose the correct alternative corresponding to the object distance 'u', image distance 'v' and the focal length 'F' of a converging lens from the following .
(i) The average speed of the image as the object moves with the uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with same speed from distance F2toF4
(ii) The minimum distance between a real object and its real image in case of a converging lens is 4F where F is its focal length.View SolutionShown an object and its image formed by a thin lens. Then the nature and focal length of lens is
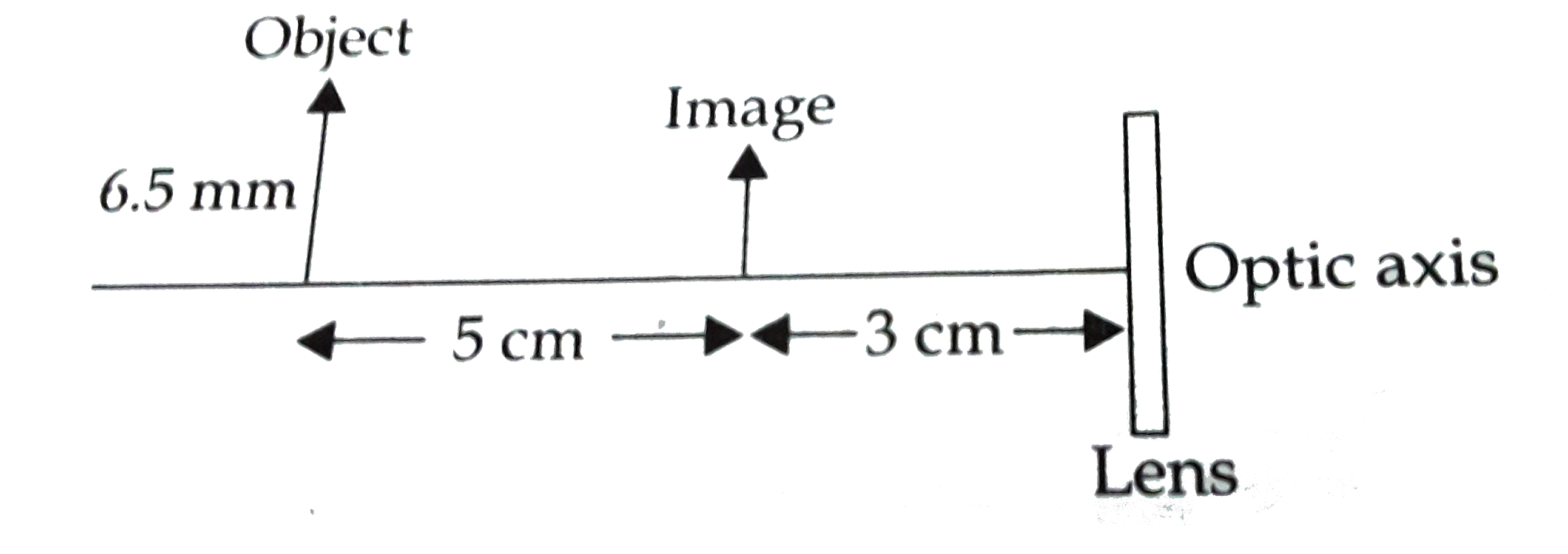 View Solution
View SolutionChoose the following statement a True of False.
a. The real image formed by a lens is always inverted.
b. The image formed by a lens is always inverted.
c. The image formed by a concave lens is always erect and diminished.
d. An air bubble inside water acts like a concave lens.
e. The distance between a real object and its real image formed by a single lens cannot be more than 4f.
f. I an object is moved at a constant speed toward a convex lens from infinity to focus, then its image moves slower in the begninning and faster later on, away from the lens.
g. The focal length of a glass (μ=1.5) lens is 10 cm in air. When it is completely immersed in water its focal length will become 40cm.View SolutionAn object is kept at rest on the principal axis of a lens. Initially the object is at a distance three times the focal length 'f' of the lens. The lens runs towards the object at a constant speed u, until the distance between the object and its real image becomes 4f. If the iamge always forms on a moving screen then express the velocity of the screen as a function of time.
View SolutionWhen an object is placed 40cm from a diverging lens, its virtual image is formed 20cm from the lens. The focal length and power of lens are
View Solution

