A galvanometer of resistance is shunted by a resistor. What part of the main current flows through the meter ?
To solve the problem, we need to determine what part of the main current flows through the galvanometer when it is shunted by a resistor of equal resistance. Let's break it down step by step.
1. Identify Given Values:
- Resistance of the galvanometer, Rg=30Ω
- Resistance of the shunt resistor, Rs=30Ω
2. Define Total Current:
- Let the total current flowing in the circuit be I.
- Let the current flowing through the galvanometer be Ig.
- The current flowing through the shunt resistor will then be I−Ig.
3. Use Kirchhoff's Voltage Law:
- The voltage across the galvanometer (Vg) is the same as the voltage across the shunt resistor (Vs) because they are in parallel.
- Therefore, we can write:
Vg=Ig⋅Rg
Vs=(I−Ig)⋅Rs
- Since Vg=Vs, we can set these two equations equal to each other:
Ig⋅Rg=(I−Ig)⋅Rs
4. Substitute the Values:
- Substitute Rg and Rs into the equation:
Ig⋅30=(I−Ig)⋅30
5. Simplify the Equation:
- We can cancel out the 30 from both sides:
Ig=I−Ig
- Rearranging gives:
Ig+Ig=I
2Ig=I
6. Solve for Ig:
- Divide both sides by 2:
Ig=I2
7. Determine the Part of the Main Current:
- The part of the main current that flows through the galvanometer is:
IgI=I2I=12
Final Answer:
Thus, the part of the main current that flows through the galvanometer is 12 or 50%.
- Resistance of the galvanometer, Rg=30Ω
- Resistance of the shunt resistor, Rs=30Ω
- Let the total current flowing in the circuit be I.
- Let the current flowing through the galvanometer be Ig.
- The current flowing through the shunt resistor will then be I−Ig.
- The voltage across the galvanometer (Vg) is the same as the voltage across the shunt resistor (Vs) because they are in parallel.
- Therefore, we can write:
Vg=Ig⋅Rg
Vs=(I−Ig)⋅Rs
- Since Vg=Vs, we can set these two equations equal to each other:
Ig⋅Rg=(I−Ig)⋅Rs
- Substitute Rg and Rs into the equation:
Ig⋅30=(I−Ig)⋅30
- We can cancel out the 30 from both sides:
Ig=I−Ig
- Rearranging gives:
Ig+Ig=I
2Ig=I
- Divide both sides by 2:
Ig=I2
- The part of the main current that flows through the galvanometer is:
IgI=I2I=12
Thus, the part of the main current that flows through the galvanometer is 12 or 50%.
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -II)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )
19 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionWe have a galvanometer of resistance 25Ω. It is shunted by a 2.5Ω wire. The part of total current that flows through the galvanometer is given as
View SolutionA galvanometer of resistance 150 ohm is shunted such that only 1/11 of the main current flows through the galvanometer. The resistance of the shunt is, (in ohm)
View SolutionA galvanometer of resistance G is shunted by a resistance Sohm. To keep the main current in the circuit uncharged, the resistnace to be put in series with the galvonmeter
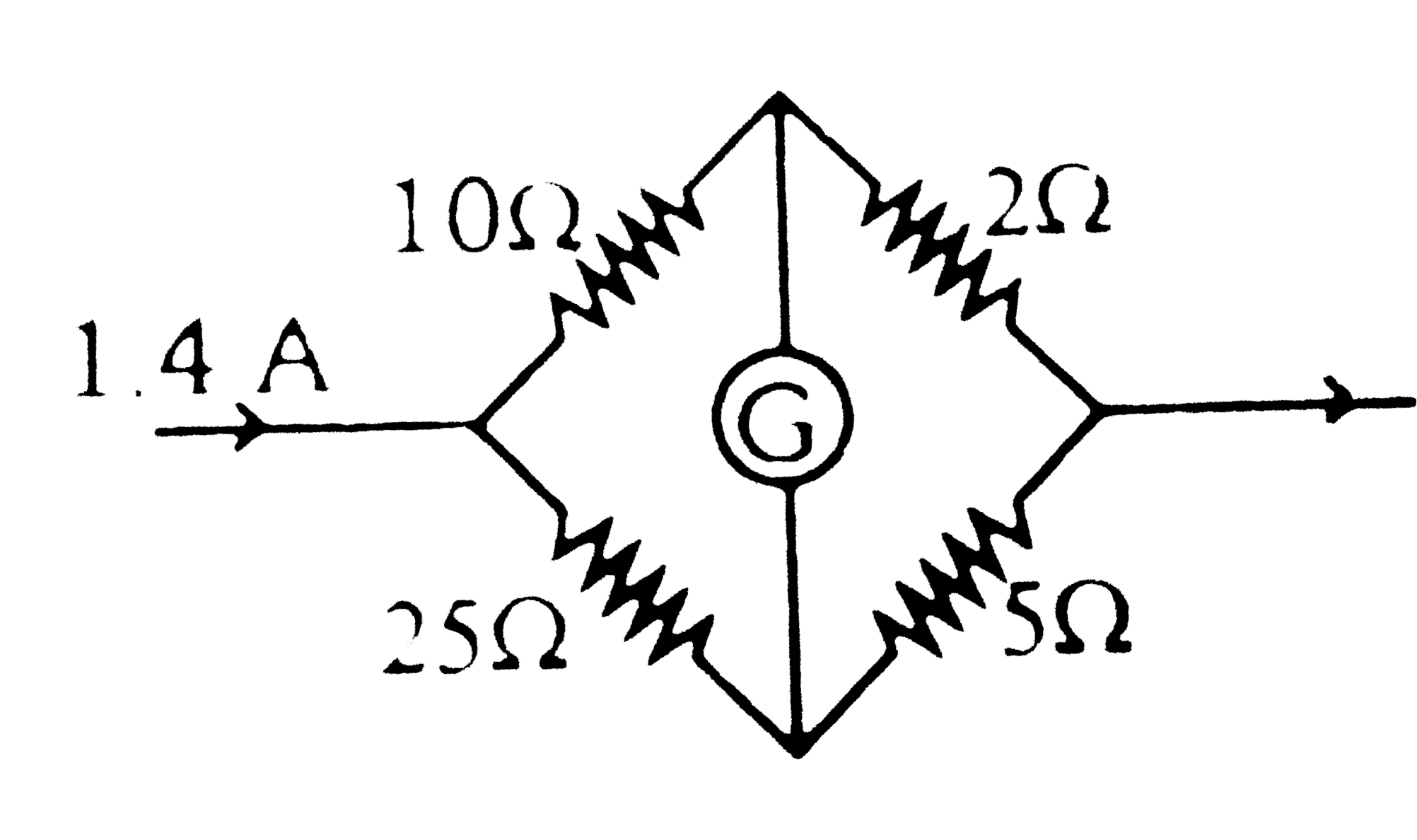
View SolutionCalculate the current flows through resistance 2Ω.
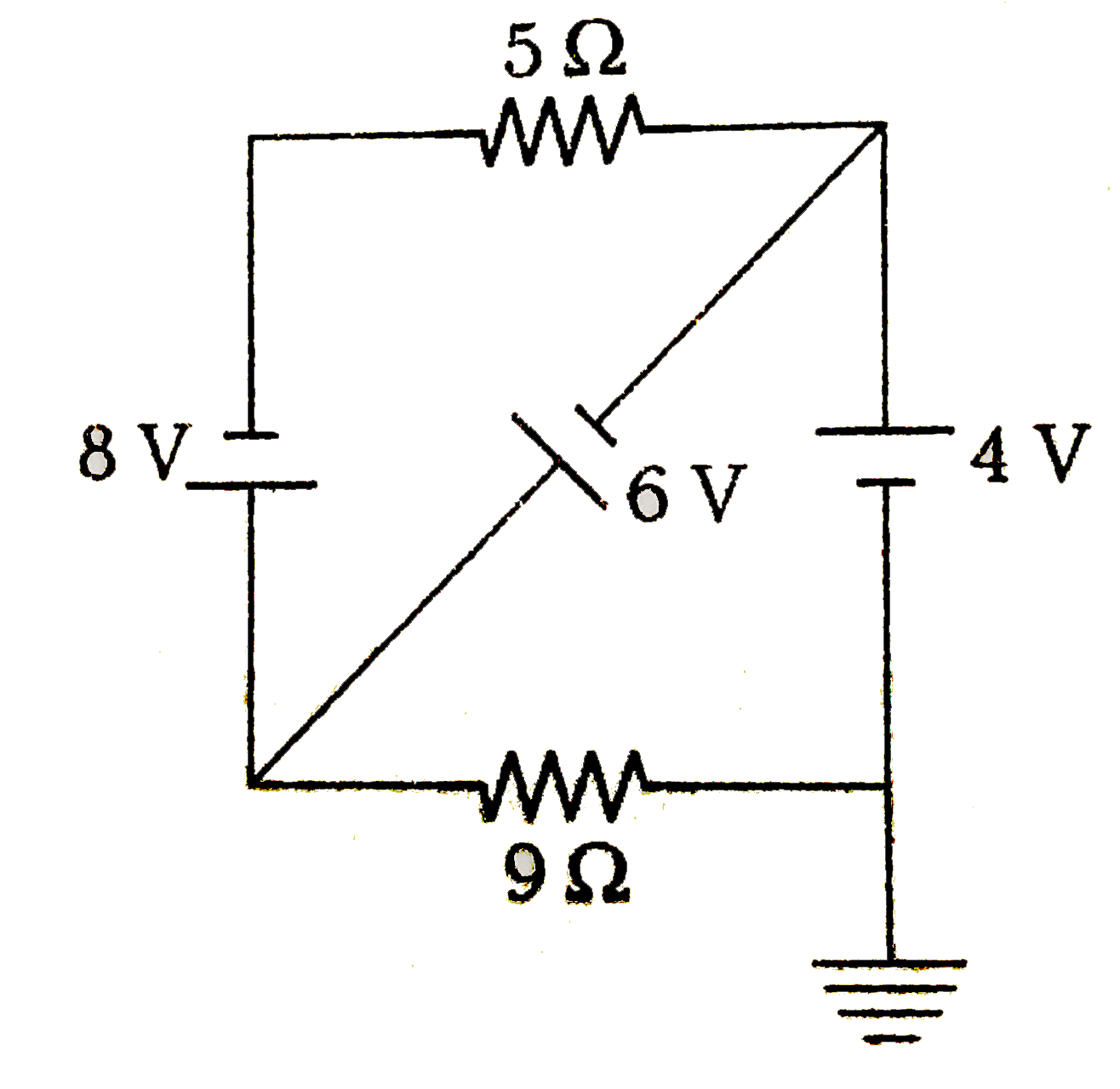
View SolutionThe current through the 5Ω resistor is
View SolutionA galvanometer has resistance 36Ω if a shunt of 4Ω is added with this, then fraction of current that passes through galvanometer is:
View SolutionCurrent through the 5Ω resistor is
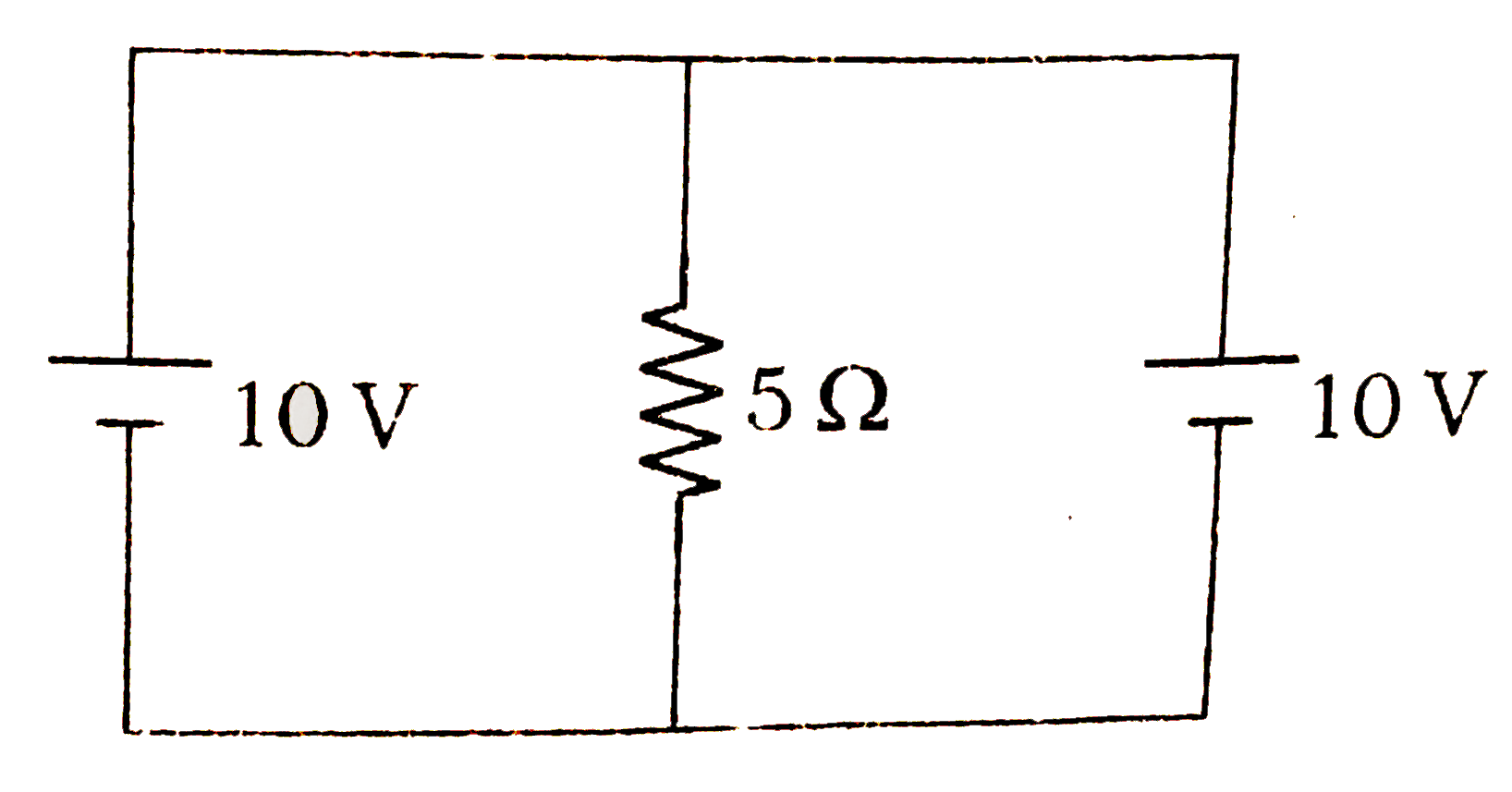
View SolutionA galvanometer coil has a resistance of 100Ω. When a current passes through the galvanometer, 1% of the current goes through the coil and the rest through the shunt. Find the resistance of the shunt.
View SolutionA galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View Solution
