In a metre bridge, the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?
To solve the problem step by step, we will first determine the resistance of resistor X using the balance point of the metre bridge. Then, we will discuss why thick copper strips are used for connections in a Wheatstone or metre bridge.
Step 1: Understand the Balance Condition of the Meter Bridge
The balance condition of a metre bridge is given by the formula:
XY=100−L1L1
where:
- X is the resistance of the unknown resistor,
- Y is the resistance of the known resistor,
- L1 is the distance from end A to the balance point.
Step 2: Substitute the Known Values
From the problem, we have:
- Y=12.5Ω
- L1=39.5cm
Now we can substitute these values into the balance condition equation.
Step 3: Calculate 100−L1
First, calculate 100−L1:
100−L1=100−39.5=60.5cm
Step 4: Substitute into the Balance Condition Equation
Now, substituting the values into the balance condition equation:
X12.5=60.539.5
Step 5: Cross-Multiply to Solve for X
Cross-multiplying gives:
X⋅39.5=12.5⋅60.5
Step 6: Calculate 12.5⋅60.5
Calculating the right side:
12.5⋅60.5=756.25
Step 7: Solve for X
Now we can solve for X:
X=756.2539.5
Calculating this gives:
X≈19.14Ω
Conclusion for Part 1
The resistance of X is approximately 19.14Ω.
---
Part 2: Why are Connections Made of Thick Copper Strips?
The connections between resistors in a Wheatstone or metre bridge are made of thick copper strips to minimize the resistance of the connecting wires. This is important because:
1. Minimizing Resistance: Thick copper strips have lower resistance compared to thinner wires, which ensures that the total resistance in the circuit is primarily due to the resistors being measured rather than the connections.
2. Accuracy: Lower resistance in connections leads to more accurate measurements, as the bridge formula assumes that the resistance of the connecting wires is negligible.
3. Heat Dissipation: Thick copper strips can also handle higher currents without overheating, making them safer and more reliable.
The balance condition of a metre bridge is given by the formula:
- X is the resistance of the unknown resistor,
- Y is the resistance of the known resistor,
- L1 is the distance from end A to the balance point.
From the problem, we have:
- Y=12.5Ω
- L1=39.5cm
First, calculate 100−L1:
Now, substituting the values into the balance condition equation:
Cross-multiplying gives:
Calculating the right side:
Now we can solve for X:
The resistance of X is approximately 19.14Ω.
The connections between resistors in a Wheatstone or metre bridge are made of thick copper strips to minimize the resistance of the connecting wires. This is important because:
2. Accuracy: Lower resistance in connections leads to more accurate measurements, as the bridge formula assumes that the resistance of the connecting wires is negligible.
3. Heat Dissipation: Thick copper strips can also handle higher currents without overheating, making them safer and more reliable.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)27videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)3videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)16videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
Similar Questions
(i) In a metre bridge, the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5Ω. Determine the resistance of X. Made of thick copper strips?
(ii). Determine the balance point of the bridge above if X and Y are interchanged.
(iii). what happens if the galvanometer and cell are interchanged at the balance point of the bridge ? Would the galvanometer show any current?View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
View SolutionIn a meter bridge,
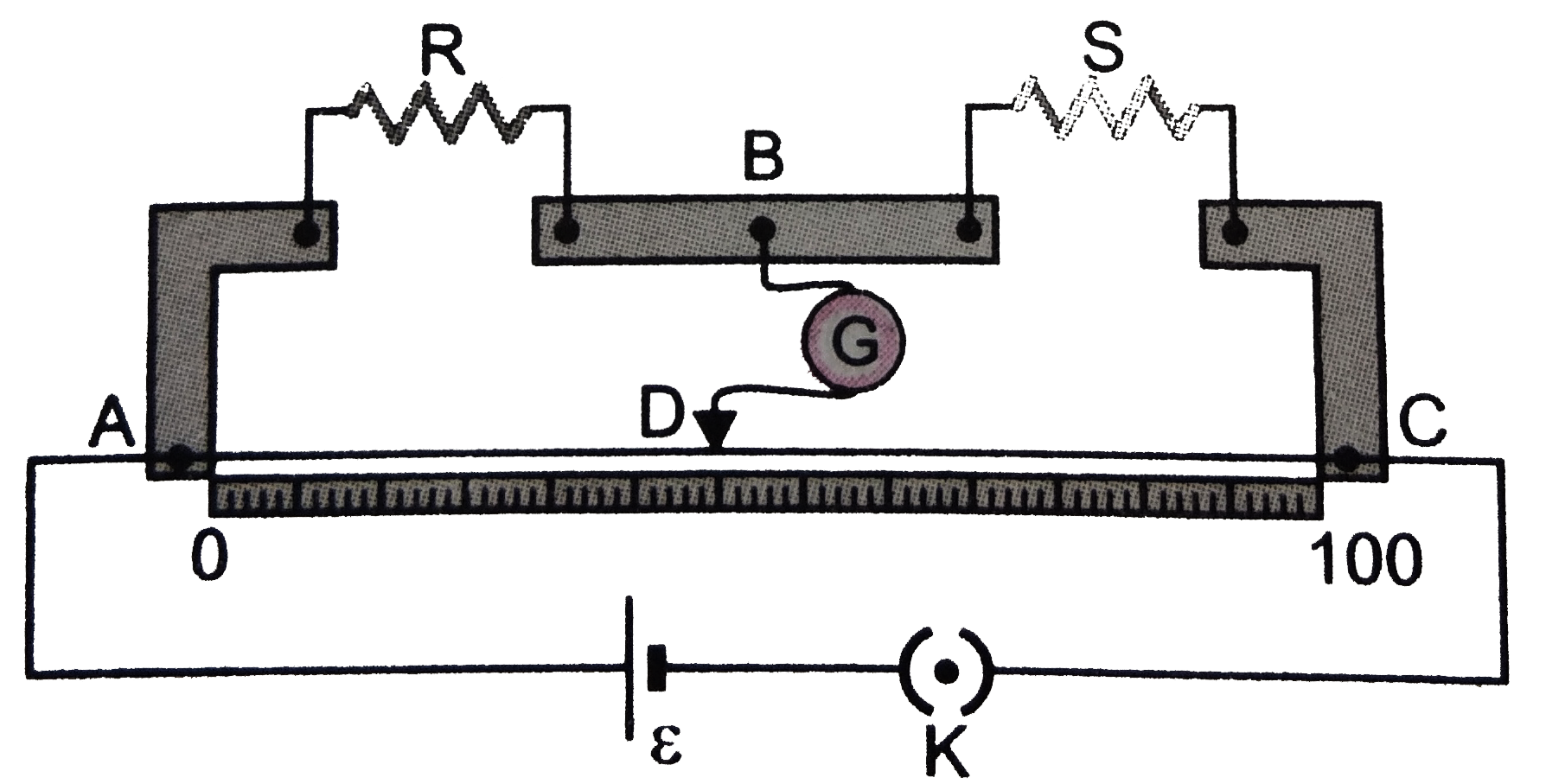
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.View SolutionIn a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
View SolutionThe figure
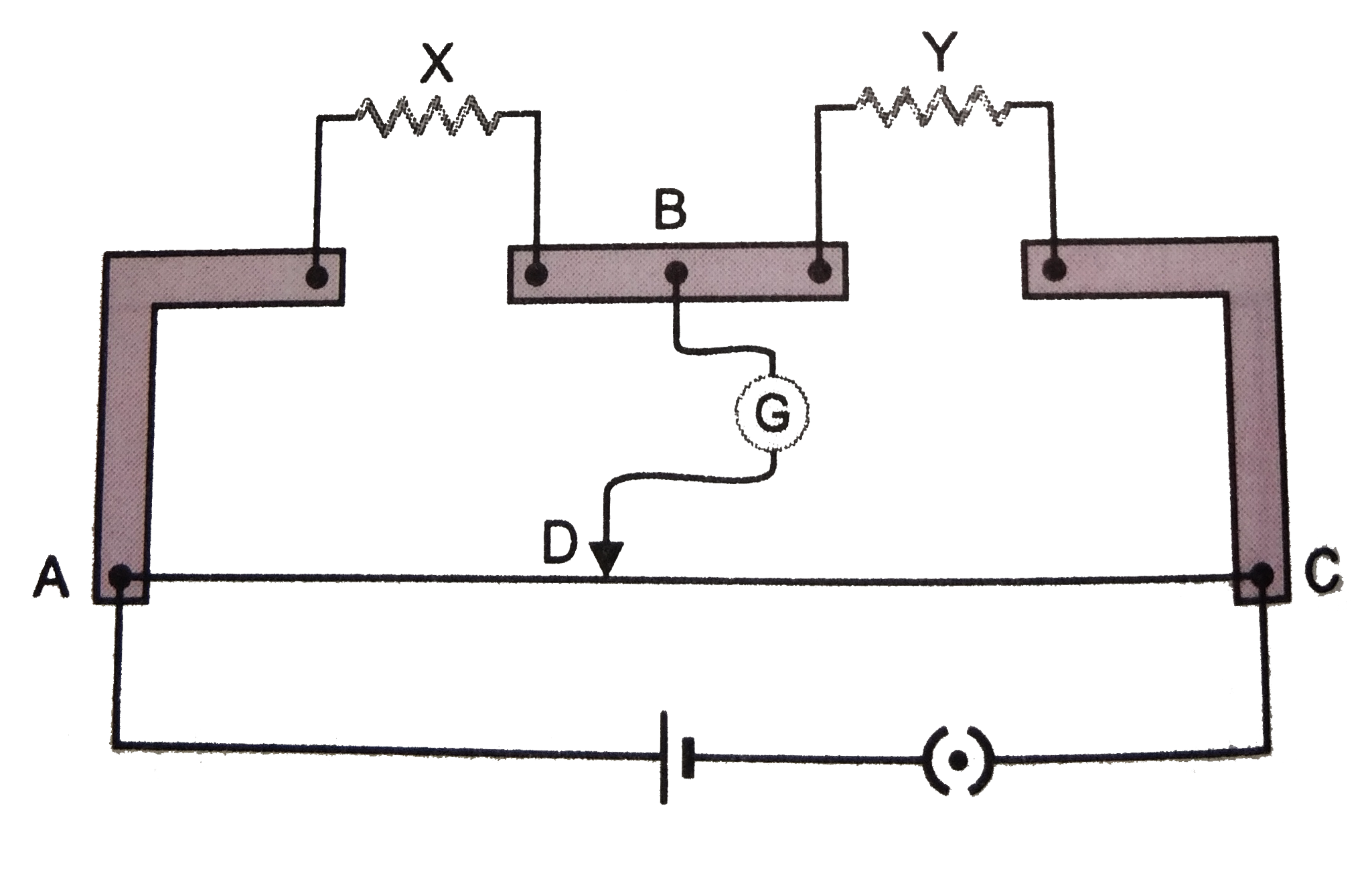
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.View SolutionIn a meter bridge, null point is at l=33.7cm, when the resistance S is shunted by 12Ω resitance the null point is found to be shifted by a distance of 18.2cm. The value of unknown resistance R should be
 View Solution
View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S
 View Solution
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.
 View Solution
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View Solution

