If the combination is connected to a battery of emf 30 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.(here R1=ohm, R2=5ohm and R3=6ohm)
To solve the problem, we need to determine the current through each resistor and the total current drawn from the battery when connected to a combination of resistors. The given resistances are R1=3Ω, R2=5Ω, and R3=6Ω, and the battery voltage (emf) is V=30V.
Step 1: Determine the Equivalent Resistance
Since the resistors are connected in parallel, we can find the equivalent resistance Req using the formula for resistors in parallel:
1Req=1R1+1R2+1R3
Substituting the values:
1Req=13+15+16
Step 2: Calculate Each Term
Calculating each term:
13=0.333,15=0.2,16≈0.167
Adding these together:
1Req≈0.333+0.2+0.167=0.7
Step 3: Find the Equivalent Resistance
Now, we can find Req:
Req=10.7≈1.43Ω
Step 4: Calculate Total Current from the Battery
Using Ohm's Law, the total current I drawn from the battery can be calculated as:
I=VReq=30V1.43Ω≈20.98A≈21A
Step 5: Calculate Current Through Each Resistor
Now, we will calculate the current through each resistor using Ohm's Law I=VR.
1. Current through R1:
I1=VR1=30V3Ω=10A
2. Current through R2:
I2=VR2=30V5Ω=6A
3. Current through R3:
I3=VR3=30V6Ω=5A
Summary of Results
- Total current drawn from the battery: I≈21A
- Current through R1: I1=10A
- Current through R2: I2=6A
- Current through R3: I3=5A
Since the resistors are connected in parallel, we can find the equivalent resistance Req using the formula for resistors in parallel:
Calculating each term:
Now, we can find Req:
Using Ohm's Law, the total current I drawn from the battery can be calculated as:
Now, we will calculate the current through each resistor using Ohm's Law I=VR.
I1=VR1=30V3Ω=10A
I2=VR2=30V5Ω=6A
I3=VR3=30V6Ω=5A
- Total current drawn from the battery: I≈21A
- Current through R1: I1=10A
- Current through R2: I2=6A
- Current through R3: I3=5A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)27videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)3videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)16videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
Similar Questions
(a) Three resistors 2Ω,4Ωand5Ω are combined in parallel. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.View SolutionA series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depends upon
View Solution
Knowledge Check
- Question 1 - Select One
Three resistors 2Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 20V and negligible internal Resistance. The total current drawn from the battery is
A10AB15AC19AD23A - Question 2 - Select One
Three resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4,3,2.4B8,7,3,4C2,5,1,8D5,5,8,2
A battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionThree resistors are connected to a 12 V battery as shown in the figure given below :
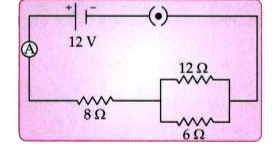
What is the current through the 6 ohm resistor ?View SolutionThree resistors are connected to a 12 V battery as shown in the figure given below :

What is the current through the 8 ohm resistor ?View SolutionTwo resistors of 2.0 92 and 3.0 22 are connected
in parallel, with a battery of 60 V and negligible internal resistance. For each case draw a circuit diagram and calculate the current through the batteryView SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,View SolutionThree resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.View Solution

