In a metre bridge, the balance point is found to be at39.5cm from the end A, when the resistor Y is of 12.5Ω.(value of X=19.14Ω) Determine the balance point of the above bridge if X and Y are interchanged.
To solve the problem, we will use the principle of a meter bridge, which is based on the Wheatstone bridge concept. The balance point in a meter bridge is determined by the ratio of the resistances on either side of the bridge.
1. Identify the Given Values:
- Balance point when Y = 12.5Ω is at L1 = 39.5 cm from end A.
- Resistance X = 19.14Ω.
2. Understand the Balance Point Relation:
The balance point (L1) in a meter bridge is given by the formula:
XY=L1100−L1
where L1 is the distance from end A to the balance point.
3. Calculate the Ratio of Resistances:
Substituting the known values into the formula:
19.1412.5=39.5100−39.5
4. Determine the New Balance Point:
When X and Y are interchanged, the new balance point (let's call it L2) will be given by:
YX=L2100−L2
Substituting the values of X and Y:
12.519.14=L2100−L2
5. Cross-Multiply and Solve for L2:
Cross-multiplying gives:
12.5(100−L2)=19.14L2
Expanding this:
1250−12.5L2=19.14L2
Combining like terms:
1250=19.14L2+12.5L2
1250=31.64L2
Now, solving for L2:
L2=125031.64≈39.5 cm
6. Calculate the New Balance Point:
The new balance point, when X and Y are interchanged, will be:
L2=100−39.5=60.5 cm
Final Answer:
The balance point of the bridge when X and Y are interchanged is 60.5 cm from end A.
- Balance point when Y = 12.5Ω is at L1 = 39.5 cm from end A.
- Resistance X = 19.14Ω.
The balance point (L1) in a meter bridge is given by the formula:
XY=L1100−L1
where L1 is the distance from end A to the balance point.
Substituting the known values into the formula:
19.1412.5=39.5100−39.5
When X and Y are interchanged, the new balance point (let's call it L2) will be given by:
YX=L2100−L2
Substituting the values of X and Y:
12.519.14=L2100−L2
Cross-multiplying gives:
12.5(100−L2)=19.14L2
Expanding this:
1250−12.5L2=19.14L2
Combining like terms:
1250=19.14L2+12.5L2
1250=31.64L2
Now, solving for L2:
L2=125031.64≈39.5 cm
The new balance point, when X and Y are interchanged, will be:
L2=100−39.5=60.5 cm
The balance point of the bridge when X and Y are interchanged is 60.5 cm from end A.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)27videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)3videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)16videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
Similar Questions
(i) In a metre bridge, the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5Ω. Determine the resistance of X. Made of thick copper strips?
(ii). Determine the balance point of the bridge above if X and Y are interchanged.
(iii). what happens if the galvanometer and cell are interchanged at the balance point of the bridge ? Would the galvanometer show any current?View SolutionTwo unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
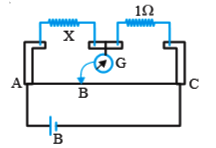 View Solution
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
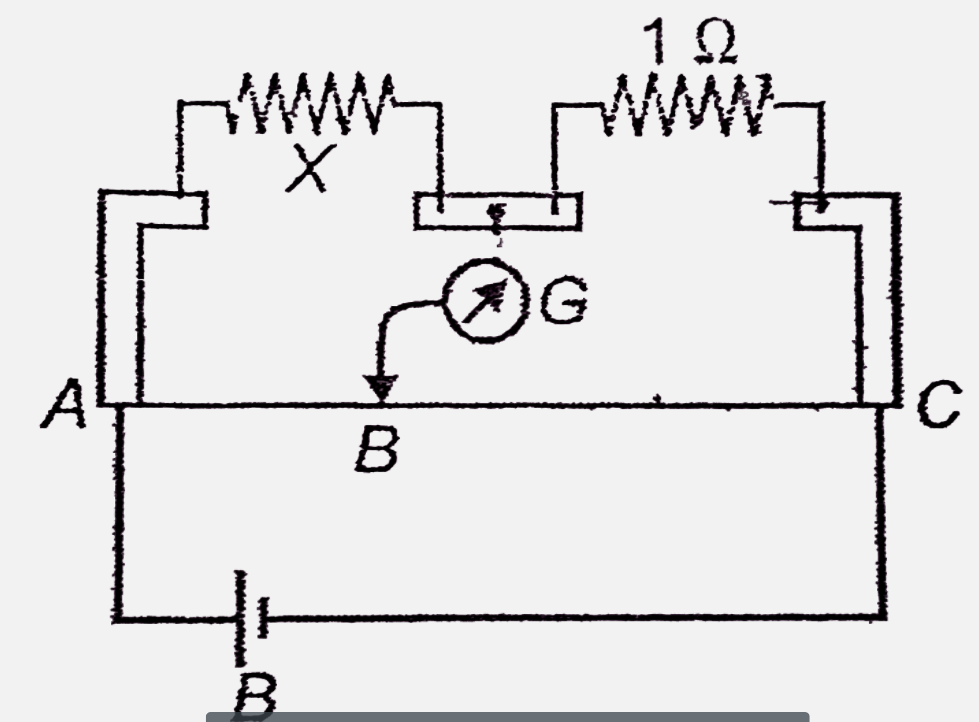 View Solution
View SolutionIn a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
View SolutionAnswer the following:
(a) Write the principle of working of a metre bridge.
(b) In a metre bridge, the balance point is found at a distance I1 with resistances R and S as shown in the figure.

An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance I2 , Obtain a formula for X in terms of I1,I2 and S .View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View Solution

