If the combination is connected to a battery of emf 24 V and negligible internal resistance, obtain the potential drop across each resistor.(here R1=1ohm,R2=ohm and R3=3ohm)
To solve the problem of finding the potential drop across each resistor when connected to a 24 V battery, we can follow these steps:
Step 1: Identify the Total Resistance
The resistors R1, R2, and R3 are connected in series. Therefore, the total resistance Rt can be calculated as:
Rt=R1+R2+R3
Given:
- R1=1Ω
- R2=2Ω
- R3=3Ω
Calculating:
Rt=1+2+3=6Ω
Step 2: Calculate the Current in the Circuit
Using Ohm's Law, the current I in the circuit can be calculated using the formula:
I=VRt
Where V=24V (the emf of the battery).
Calculating:
I=24V6Ω=4A
Step 3: Calculate the Potential Drop Across Each Resistor
Now, we can calculate the potential drop across each resistor using Ohm's Law V=I×R.
1. Potential Drop Across R1:
VR1=I×R1=4A×1Ω=4V
2. Potential Drop Across R2:
VR2=I×R2=4A×2Ω=8V
3. Potential Drop Across R3:
VR3=I×R3=4A×3Ω=12V
Final Results
- The potential drop across R1 is 4V.
- The potential drop across R2 is 8V.
- The potential drop across R3 is 12V.
The resistors R1, R2, and R3 are connected in series. Therefore, the total resistance Rt can be calculated as:
Rt=R1+R2+R3
Given:
- R1=1Ω
- R2=2Ω
- R3=3Ω
Rt=1+2+3=6Ω
Using Ohm's Law, the current I in the circuit can be calculated using the formula:
I=VRt
Where V=24V (the emf of the battery).
I=24V6Ω=4A
Now, we can calculate the potential drop across each resistor using Ohm's Law V=I×R.
VR1=I×R1=4A×1Ω=4V
VR2=I×R2=4A×2Ω=8V
VR3=I×R3=4A×3Ω=12V
- The potential drop across R1 is 4V.
- The potential drop across R2 is 8V.
- The potential drop across R3 is 12V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)
3 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
(a) Three resistors 1Ω,2Ω and 3Ω are combined in series. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View Solution
Knowledge Check
Three resistances 2Ω,4Ω,5Ω are combined in series and this combination is connected to a battery of 12 V emf and negligible internal resistance. The potential drop across these resistances are
A(5,45,4.36,2.18)VB(2,18,5.45,4.36)VC(4.36,2.18,5.45)VD(2.18,4.36,5.45)VThree resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4,3,2.4B8,7,3,4C2,5,1,8D5,5,8,2
A resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
View SolutionThree resistors are connected to a 6 V battery as shown in the figure
Calculate:
potential difference across the 7.2 ohm resistor
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionFigure below shows two resistors R1andR2 connected to a battery having an emf of 40 V and negligible internal resistance. A voltmeter having a resistance of 300 Ω is used to measure potential difference across R1 Find the reading of the voltmeter.

View SolutionTwo resistances of 100 ohm and 200 ohm are connected in series with a battery of emf 4 volt and negligible internal resistance. A voltmeter of resistance 200 ohm is used to measure voltage across the two resistances separately. Calculate the voltage indicated.
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
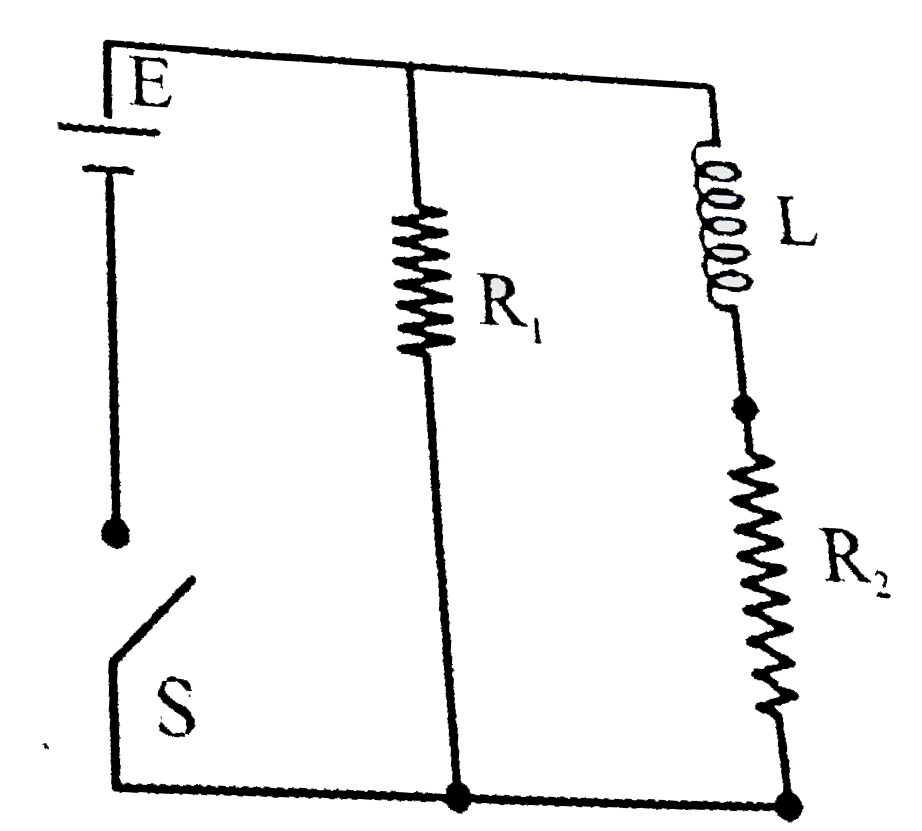
View Solution
