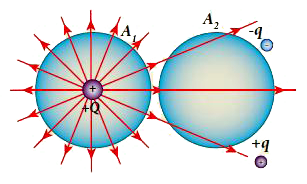
In figure , calculate the electric flux through the closed areas $A_{1} and A_{2}$ .

Text Solution

Verified by Experts

In figure (a), the area $A_{1}$ encloses the charge Q. So electric flux through this closed surface $A_{1}$ is $\frac{Q}{ε_{o}}$ . But the closed surface $A_{2}$ contains no charges inside, so electric flux through $A_{2}$ is zero.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

BOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION (Multiple choice questions)
15videos
ELECTROSTATICS
BOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - Exercises
23videos
ELECTROSTATICS
BOOK - NCERT TAMILCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ADDITIONAL EXERCISES
1videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
BOOK - NCERT TAMILCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - EVALUATION (IV. Numerical problems)
10videos
MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT

Similar Questions

Knowledge Check

Question 1 - Select One
The total electric flux $ϕ$ through the entire area of a closed surface is given by
A $ϕ = \oint \to E \times \to d s$
B $ϕ = \oint \to E \cdot \to d s$
Cboth 'a' and 'b'
Dnone of these
Question 2 - Select One
The electric flux through a closed surface area S enclosing charge Q is $ϕ$ If the surface area is doubled, then the flux is
A $2 ϕ$
B $ϕ / 2$
C $ϕ / 4$
D $ϕ$
Question 3 - Select One
The capacitance of the capacitors of plate areas $A_{1}$ and $A_{2} (A_{1} < A_{2})$ at a distance d is

A $\frac{ε_{0} A_{1}}{d}$
B $\frac{ε_{0} A_{2}}{d}$
C $\frac{ε_{0} (A_{1} + A_{2})}{2 d}$
D $\frac{ε_{0} \sqrt{A_{1} A_{2}}}{d}$

NCERT TAMIL-ELECTROSTATICS-Exercises

Home
Ask Doubt
Profile