How does the wave y=sin(x-a) for a = 0 , $a = \frac{π}{4}, a = \frac{π}{2}, a = \frac{3 π}{2}$ and $a = π$ look like? Sketch this wave.

Text Solution

Verified by Experts

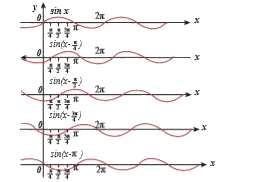
From the above picture we observe that
y=sin(x-a) for a = 0, $a = \frac{π}{4}, a = \frac{π}{2}, a = \frac{3 π}{2}$ and $a = π$ , the function y=sin(x-a) shifts towards right. Further, we can take a=vt and $v = \frac{π}{4}$ , and sketching for different times t = 0 s , t = 1 s, t = 2 s etc., we once again observe that y = sin(x-vt) moves towards the right. Hence, y=sin(x-vt) is a travelling (or progressive) wave moving towards the right. If y= sin(x+vt) then the travelling (or progressive) wave moves towards the left. Thus, any arbitrary function of type y = f(x-vt) characterising the wave must move towards right and similarly, any arbitrary function of type y = f(x+vt) characterizing the wave must move towards left.

A transverse wave is described by the equatiion $Y = Y_{0} sin 2 π (f t - x / λ)$ . The maximum particle velocity is equal to four times the wave velocity if
$λ = π Y_{0} / 4$
$λ = π Y_{0} / 2$
$λ = π Y_{0}$
$λ = 2 π Y_{0}$
A $λ = π Y_{0} / 4$
B $λ = π Y_{0} / 2$
C $λ = π Y_{0}$
D $λ = 2 π Y_{0}$
The equation of a progressive wave is $y = 4 sin (4 π t - 0.04 x + \frac{π}{3})$ where x is in metre and t is in second. The velocity of the wave is
A $100 π m s^{- 1}$
B $50 π m s^{- 1}$
C $25 π m s^{- 1}$
D $π m s^{- 1}$
A transverse wave propagating along x-axis is represented by: $y (x, t) = 8.0 sin (0.5 π x - 4 π t - \frac{π}{4})$ Where $x$ is in metres and $t$ is in seconds. The speed of the wave is:
A $4 π m / s$
B $0.5 π m / s$
C $\frac{π}{4} m / s$
D $8 m / s$