If along a uniform rod of length l carrying current i the voltage V changes with position x along the length of the rod such that dVdx=−k where k is a positive number then the resistance of the rod is
kl/2I
kl/I
I/kl
klI
The correct Answer is:B
dV=−IdR−IρdxA
dVdx=−IρA=−k
⇒R=kl/I
II Method:
V2_V1=∫(dVdl)dl=kL=IR
Topper's Solved these Questions
Similar Questions
If linear density of a rod of length 3m varies as λ=2+x, them the position of the centre of gravity of the rod is
View SolutionA uniform thin rod of length 3L is bent at right angles at a distance L from one end as shown in Fig. If length of rod is 1.8m, find the co-ordinates and position vector of the mass of the system.

View Solution
Knowledge Check
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLIn the figure shown a uniform rod of length l and mass m is kept at rest in horizontal position on an elevated edge. The value of x is such that the rod will have maximum angular acceleration α, as soon as it is set free.
Ax is equal to l2√3Bα is equal to g√32lCα is equal to g√3lDx is equal to l√3A rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
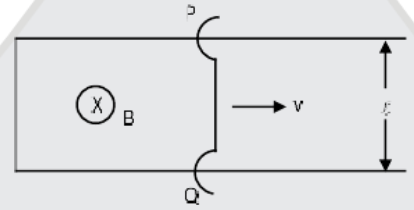 A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
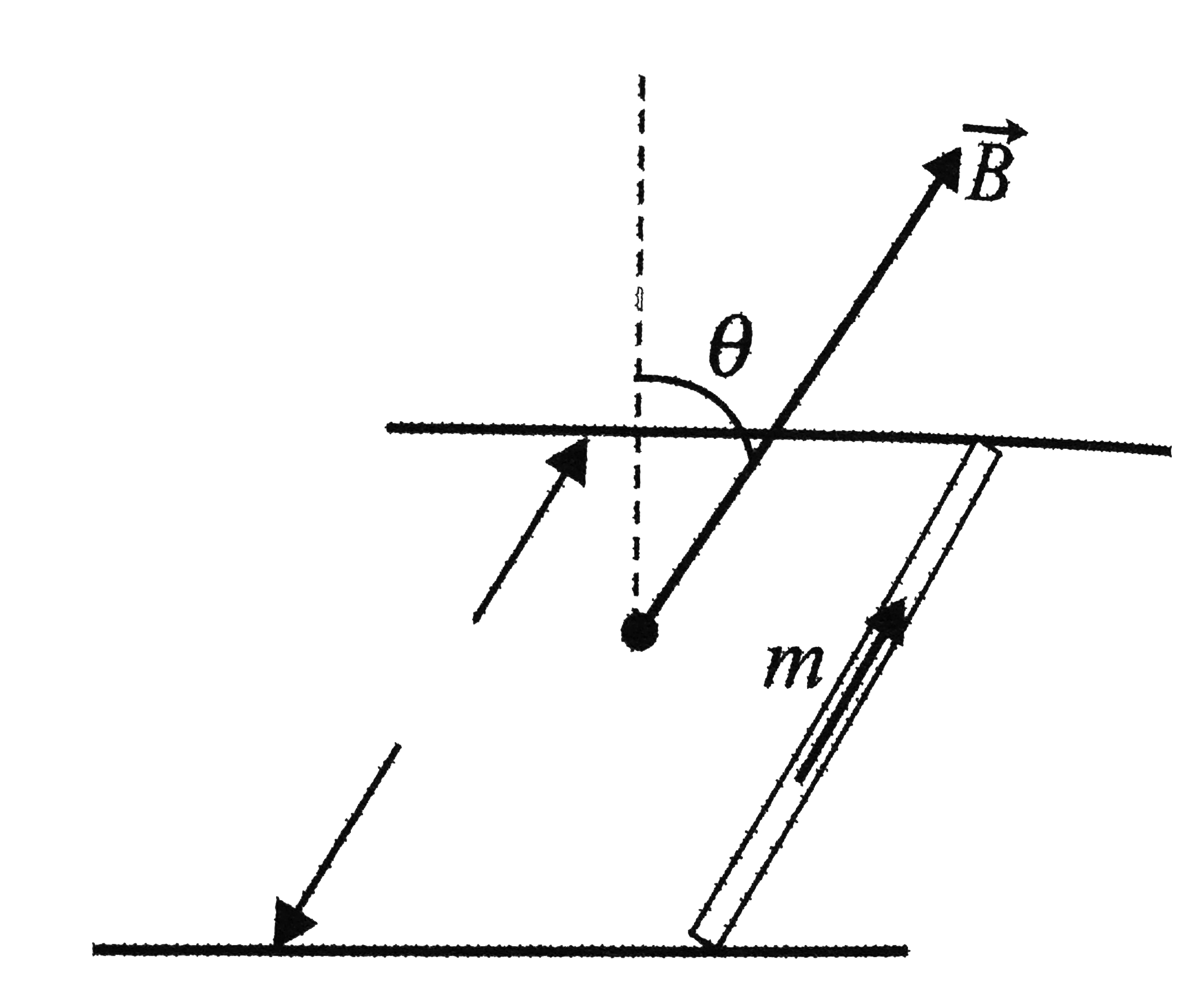
View SolutionA metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.

View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThe mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is
View Solution